システム事業部 廣澤 邦一、中川 博
1. はじめに
近年、多孔質弾性材料を主とした新たな音響材料のニーズが高まっており、この傾向は特に自動車業界で顕著になっております。 このような開発現場においては、より薄くより軽い材料でかつ吸遮音性能がよいという音響特性を求め、 様々な材料を積層させるのが一般的であり、また効率的です。したがって開発効率を上げるため、 積層構造に対応した音響性能を予測するソフトウェアが求められますが、このようなソフトウェアは非常に少ないという問題が存在します。 また、より高精度に予測するための手法も存在しますが、高精度になるほど予測手法が複雑になり扱い難くなる問題もあります。 そこで当社では、高精度に多孔質弾性材料を取り扱うことができるBiotモデル[1-3]を導入し、 さらに積層構造に対応する音響性能予測ソフトウェアCapMLS (Calculation of Acoustical Properties for MultiLayer Structures) を開発しましたので、 ここでご紹介いたします。
2. ソフトウェアの概要
CapMLSは伝達マトリックス法を用いた数値計算[1,7]により、無限面積の多層積層構造に平面波が入射する場合の音響特性を求めることができます。 音波の入射角度を自由に設定することができるため、図1に示すような垂直入射、斜入射および統計入射について予測することができます。 また図2に示すように、音波が入射する領域と反対側の領域を、音が透過していく空気の場合と、 音波が全く透過しない非通気性の剛壁の場合の2種類から選択できます。したがって、透過損失を計算する場合は透過性にし、 音響管の実測値と比較するために剛壁にして計算するというように使い分けることができます。
CapMLSが取り扱うことのできる積層構造を構成する材料のモデルは、Fluid、Elastic(impervious)、 Porous(Biot model)およびPorous(Equivalent fluid model)の4種類です。
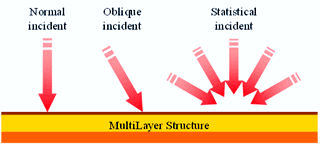
図1:各入射条件のイメージ
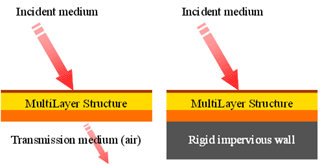
図2:終端条件のイメージ;
(左) 透過性、(右) 非通気性剛壁

図3:材料と材料の接着状態による振動伝搬の絶縁のイメージ;
(左) 接着状態、(右) 非接着状態
これらのモデルを組み合わせることによって自由に積層構造を構築することができます。各モデルの特徴は表1の通りです。
CapMLSの最大の特徴であるPorous(Biot model)[2,3,10]は、多孔質材料の弾性も考慮することができるため、 音波によって励振された多孔質材料自身の振動もシミュレーションできます。これに関連して、CapMLSはある材料と材料が完全に接着されている状態にある場合と、 触れ合っているだけで接着されていない状態にある場合をモデル化することができます。すなわち図3に示すように、 完全に接着されている状態では、材料同士を隣り合わせることによって音波の伝達のほか振動の伝達までもモデル化できることになります。
表1:CapMLSで扱う材料のモデル
| Fluid | 気体のみで構成される材料 (例 : 空気) |
| Elastic (impervious) |
非通気性の弾性材料 (例 : 鉄やアルミなどの板、プラスティックのフィルムなど) |
| Porous (Biot model) |
多孔質材料のフレーム(骨格)の弾性を考慮したモデル (例 : グラスウール、フェルト、膜有りウレタンなど) |
| Porous (Equivalent fluid model) |
多孔質材料のフレーム(骨格)の弾性を無視したモデル (例 : グラスウール、フェルト、膜無しウレタンなど) |
図4:CapMLSの画面
これとは逆に、接着されておらず材料の振動は隣の材料に伝達されないと考えられる場合は、 ごく薄い空気層を材料と材料の間に挿入することによって振動の絶縁をモデル化することができます。 このように自由に積層構造を構築することによって、より現実的な積層構造のモデル化がCapMLSでは可能です。
CapMLSは図4のようなウィンドウ構成であり、メインウィンドウで積層構造の構築を行い、 それぞれの材料の厚さや密度などのパラメータを入力します。この各材料に対するパラメータの詳細については、 文献[8-10]をご参照ください。また当社では、各種パラメータの測定も行っておりますので、お気軽にお問い合わせください。
次に、各入射条件に対するCapMLSで計算できる評価量は以下の表2の通りです。なお、CapMLSでは計算結果を保存と読み込みができますが、 このデータファイルのフォーマットは当社製品の垂直入射吸音率測定システムWinzacで測定されたデータの出力ファイル形式と同一であるため、 測定データを読み込むことができ、計算結果と測定結果の比較検討が可能です。
表2:CapMLSで計算できる評価量
| 斜入射 | 統計入射 | |
| 吸音率 | ○ | ○ |
| 透過損失 | ○ | ○ |
| 比音響インピーダンス*1 | ○ | × |
| 複素音圧反射率 | ○ | × |
*1) CapMLSで求められる比音響インピーダンスは、積層構造表面上における
音圧と垂直方向の粒子速度の複素比を表します。
3. 数値計算例と測定結果との比較
それでは、CapMLSによる数値計算結果と実測値を比較することによってCapMLSの予測精度を検証した例を示します。
3.1 垂直入射吸音率
ここでは、CapMLSによる予測値とWinzacによる垂直入射吸音率の実測値を比較します。 比較に用いた試料は、Glass wool 96K(25t)、 Glass wool 96K(25t)にFilm(0.05t)を貼り付けたもの、 およびGlass wool 96K(25t)にRubber(1t)を貼り付けたものの3種類です。これらの計算に必要なパラメータを表3~表5に示します。
表3:Glass wool 96Kのパラメータ
| Thickness | 25 mm |
| Flow resistivity | 50000 Ns/m4 |
| Porosity | 0.96 |
| Tortuosity | 1.07 |
| VCL*2 | 50×10-6 m |
| TCL*3 | 100×10-6 m |
| Density | 96 kg/m3 |
| Shear modulus | 1.0×105 N/m2 |
| Loss factor | 0.25 |
| Poisson's ratio | 0 |
*2) Viscous Characteristic Length (粘性特性長、文献〔1,9〕参照)
*3) Thermal Characteristic Length (熱的特性長、文献〔1,9〕参照)
| Thickness | 0.05 mm |
| Density | 920 kg/m3 |
| Shear modulus | 2.6×108 N/m2 |
| Loss factor | 0.1 |
| Poisson's ratio | 0.46 |
| Thickness | 1 mm |
| Density | 1400 kg/m3 |
| Shear modulus | 1.5×105 N/m2 |
| Loss factor | 0.1 |
| Poisson's ratio | 0.46 |
また、図5にGlass wool 96K(25t)、図6にGlass wool 96K + Film(0.05t)、 図7にGlass wool 96K(25t) + Rubber(1t) のそれぞれの予測値と実測値を示します。なお、 これらの試料は材料同士が完全には接着されていないと考えられるため、材料と材料の間に非常に薄い空気層を挿入しました。 同様に測定時の音響管の剛壁と試料も非接着状態であるため、剛壁の直前にごく薄い空気層を設けて計算しました。
図5を見ると、CapMLSの予測値とWinzacによる測定値は非常によく合っていることが分かります。 また図6のFilmを加えた結果についても2kHz以上の高域を除いてよく合っています。 一方図7のRubberを加えたものに関しては吸音率のピーク周波数をよく予測しているものの、 その値や500Hz以上の周波数域に関して両者が合っているとはいえない結果となりました。 これはRubberのような粘弾性体の弾性率が周波数依存するのに対し、CapMLSはその依存性を考慮していないこと、 また音響管による測定においてRubberの音響管内における設置状態がCapMLSの前提である無限大平板を実現できないことが原因であると考えられます。 このような原因を考慮するとCapMLSの予測は比較的妥当であるといえます。なお、粘弾性体における弾性率の周波数依存性は、 今後の課題として考慮できるように更なる開発を進める予定です。
3.2 透過損失
ここでは、CapMLSによる予測値と、当社音響研究所の残響室-無響室による実測値を比較します。 比較に用いた試料はSteel (0.8t)、Steel(0.8t)にFelt(20t)とFilm(0.05t)を貼り付けたもの、およびFelt(20t)の3種類です。 SteelとFeltの計算に必要なパラメータを表6と表7に示します。またFilmのパラメータは表4の通りです。 また図8にSteel(0.8t)、図9にSteel(0.8t)+Felt(20t)+Film(0.05t)、図10にFelt(20t)のそれぞれの予測値と実測値を示します。 また、Feltのみの図10にはFelt(20t)の面密度0.8kg/m2をもとに計算した質量則(Masslaw)を併記しています。 なお、Steel(0.8t)+Felt(20t)+Film(0.05t)は、お互いの材料は完全には接着されていないと考えられるため、 材料と材料の間に非常に薄い空気層を挿入しました。
図8~10を見ると、CapMLSの予測値と実測値は500Hz以下の低周波数域を除いて非常によく合っているといえます。 低周波数域で実測値が予測値と合わなくなる原因は、現実の試料はCapMLSが前提としている無限大平板ではなく有限面積であり、 さらに試料の周辺を固定している影響であると考えられます。したがって、今回の実測に用いた試料よりも大きなものを用いて測定することで、 より予測値との整合が低周波数域まで向上すると予想されます。この面積が有限であることの影響を考慮できるような機能も開発する予定です。
| Thickness | 0.8 mm |
| Density | 7850 kg/m3 |
| Shear modulus | 8.1×1010 N/m2 |
| Loss factor | 0.001 |
| Poisson's ratio | 0.29 |
| Thickness | 20 mm |
| Flow resistivity | 19000 Ns/m4 |
| Porosity | 0.96 |
| Tortuosity | 1.07 |
| VCL*2 | 80×10-6 m |
| TCL*3 | 160×10-6 m |
| Density | 40 kg/m3 |
| Shear modulus | 1.0×105 N/m2 |
| Loss factor | 0.3 |
| Poisson's ratio | 0 |
図10では、Feltの質量則も併記していますが、この質量則はCapMLSの予測値と実測値の両方に対してまったく合っていません。 これは質量則が非通気性弾性材料に対して成り立つ法則であるにもかかわらず、 Feltという多孔質材料に用いたためにその前提条件を満たさないことが原因であると考えられます。したがって、 闇雲に質量則を用いることの危険性を示唆できるとともに、CapMLSによる予測の優位性が示されたといえます。
4. おわりに
本報では、今回新たに開発した積層構造に対する音響特性予測ソフトウェアCapMLS(Calculation of acoustical properties for MultiLayer Structures)を紹介させていただきました。このソフトウェアは気体、 非通気性弾性体および多孔質弾性体をそれぞれモデル化することができ、多くの積層構造の音響特性を予測することができます。 また多孔質弾性体のモデル化にはBiotモデルを適用するため、多孔質材料の振動伝搬も含めたより精密な予測が可能となります。 このCapMLSによる予測値は実測値とよく対応することを検証によって確認しております。
CapMLSを使用することによって、新材料を開発する段階で試料を作成することなくその材料の音響特性を予測することができるようになるため、 開発スピードを速めることができ、開発コストを削減することが可能になると考えられます。また今ある材料のパラメータを測定しデータベースとして保持していれば、 その材料の音響特性を様々な入射条件に対して予測でき、データベース内の材料の組み合わせによって新たな構造の音響特性もシミュレートすることもできます。
CapMLSをご利用いただき、それによって新たな材料開発のお手伝いができることがあれば、当社にとってこの上ない喜びであります。 前述の通り今後も更なる開発を進め、より使いやすく高機能の製品をご提供できるよう邁進していきたいと思っております。
参考文献
-
J.F.Allard, “PROPAGATION OF SOUND IN POROUS MEDIA.” (ELSEVIER APPLIED SCIENCE, LONDON and NEW YORK, 1993)
-
M.A.Biot, “Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. I. Low-Frequency Range”, J.A.S.A. Vol.28(2), pp.168-178(1956)
-
M.A.Biot, “Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. II. Higher-Frequency Range”, J.A.S.A. Vol.28(2), pp.179-191(1956)
-
D.L.Folds and C.D.Loggins, “Transmission and reflection of ultrasonic waves in layered media”, J.A.S.A. Vol.62(5), pp.1102-1109(1997)
-
Jean F.Allard, Claude Depollier, Pascal Rebillard, Walter Lauriks and Andre Cops, “Inhomogeneous Biot waves in layered media”, J.Appl.Phys. Vol.66(6), pp.2278-2284 (1989)
-
Walter Lauriks, Andre Cops, Jean F.Allard, Claude Depollier and Pascal Rebillard, “Modelization at oblique incident of layered porous materials with impervious screens”, J.A.S.A. Vol.87(3), pp.1200-1206 (1990)
-
B.Brouard, D.Lafarge, “A GENERAL METHOD OF MODELLING SOUND PROPAGATION IN LAYERED MEDIA”, J.Sound Vib. Vol.183(1), pp.129- 142(1995)
-
中川博、音響材料について、NOE技術ニュース Vol.19、pp.24-27(2003)
-
中川博、音響材料について(その2)、NOE技術ニュース Vol.21、pp.15-18(2004)
-
中川博、音響材料について(その3)、NOE技術ニュース Vol.22、pp.7-11(2005)
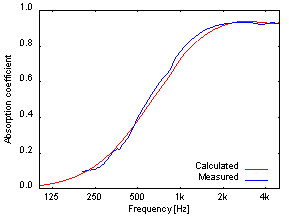
図5:GW96K(t25)に対する垂直入射吸音率の
CapMLSによる計算値とWinzacによる実測値との比較
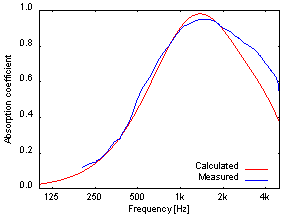
図6:GW96K(t25)+film(0.05t)に対する垂直入射吸音率の
CapMLSによる計算値とWinzacによる実測値との比較
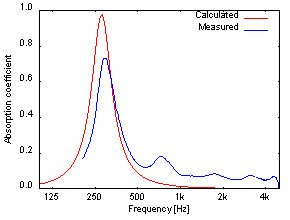
図7:GW96K(t25)+rubber(1t)に対する垂直入射吸音率の
CapMLSによる計算値とWinzacによる実測値との比較
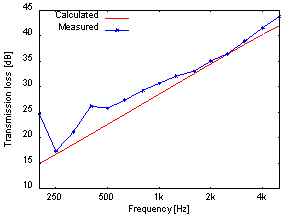
図8:鉄板(0.8t)に対する音場入射透過損失の
CapMLSによる計算値と残響室-無響室による実測値の比較
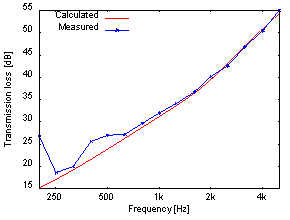
図9:Steel(0.8t)+Felt(20t)+Film(0.05t)に対する音場入射透過損失の
CapMLSによる計算値と残響室-無響室による実測値の比較
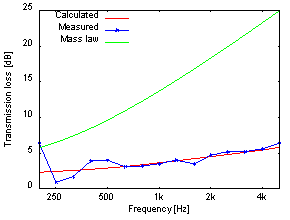
図10:Felt(20t)に対する音場入射透過損失の
CapMLSによる計算値と残響室-無響室による実測値の比較




