システム事業部 中川 博、廣澤 邦一、金 誠
1. はじめに
材料の吸音性能の評価量として代表的なものの一つが垂直入射吸音率です。その垂直入射吸音率を測定するのに通常は「音響管 (Acoustic impedance tube、あるいはKundt's tube(クント管))」を用います1)。音響管を用いるのは、管内の音場がほぼ完全な平面波音場であるとみなせ、非常に単純な測定原理に基づいて小さなサンプルで再現性の高い吸音率測定ができるからです。実際に研究分野から開発現場まで多様な環境で多孔質材料の音響特性の評価に用いられています。しかしながら、この測定方法は平坦で均質な材料を前提としているので、様々な形に成型されて平坦な面のないサンプルの測定は行うことができません。さらにあまり気づかれていませんが、音響管での測定の大きな欠点として、非通気あるいは通気の少ない層を有する材料では、切り出したサンプルの大きさに依存する固体伝搬音(振動)の影響により測定結果が変化してしまうという点があります2)。これは言い換えると、サンプルの材料特性(密度、弾性率)と大きさ(直径、厚さ)及び支持条件によって決定する固有振動が吸音に影響するということです。筆者らも以前よりこの影響を軽減する方法を提案しています3),4)が、根本的な解決とはなっていません。
そこで、音響管を使わずに材料の吸音特性を測定する方法として「自由音場法 (Free field technique) 」が提案されています5)。この方法は、音響管のような理想的な平面波音場ではないので、それを考慮した測定方法が必要となるものの、音響管では測定できない平坦でない材料や非通気層を有する材料の垂直入射吸音率や、あるいは斜め入射吸音率の測定なども可能であり、以前弊社技術ニュース6)でもご紹介したBiot-Allard7)モデルの検証(主に無響室で測定します)や施工後の室内の壁の吸音率測定(施工現場での測定)など、様々な用途への利用が期待されます。
2. 自由音場法
最初に少し数式を交えて本手法の原理的な説明をいたします。まず図1のような垂直入射条件の場合を考えます。半自由空間上に試料が設置され、試料面近傍に受音点R、さらにその上に点音源Sがあるとした場合のモデルを考えます。なお弊社では、測定用センサとして前号8)でも少しご紹介したMicroflown社のPU-probeを使用しています。
2.1 平面波近似
最も単純なモデルを考えます。音源距離が試料面から十分遠い場合、試料面への音波の入射条件を音響管と同じような平面波入射であると仮定することができます。この場合、受音点Rの音圧と測定面に対して法線方向の粒子速度は時間項ejωtを省略すると次の式で表されます。
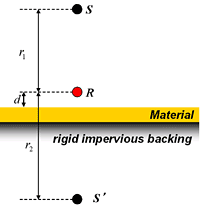
図1 鏡像音源モデル (垂直入射の場合)
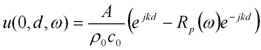
したがって受音点Rにおけるノーマル比音響インピーダンスは、次の式で表されます。
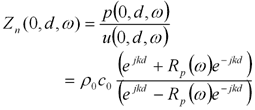
上記インピーダンスが得られれば次の式で音圧反射係数を求めることができます。
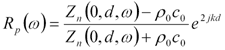
PU-probeは音圧と粒子速度を同時に測定することができるので、一度の測定で(3)式のインピーダンスを求めることができます。
2.2 平面波反射係数を用いた鏡像モデル (Surface impedance法)
続いて、図1のS'のような鏡像を考えます。ここでも音源の距離は波長にくらべて十分離れていて試料面への音波の入射はほぼ平面波入射であるとすると、音圧反射係数は平面波反射係数を用いることができます9)。このときの受音点Rにおける音圧および法線方向粒子速度は次の式で表されます。
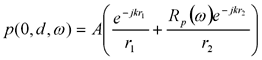 (5)
(5)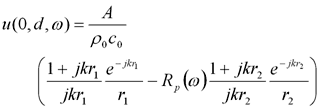 (6)
(6)このときのノーマル比音響インピーダンスは、
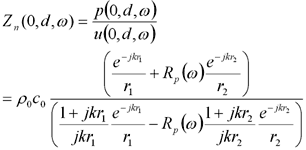 (7)
(7)よって、上記インピーダンスが得られれば音圧反射係数を求めることができます。
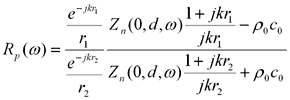 (8)
(8)
つづいて、図2のような斜め入射の場合を考えます。(8)式においてr1、r2が十分大きく(r1、r2≫kr )なると、(4)式に一致します。
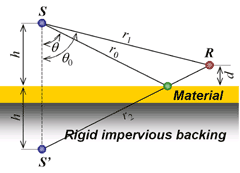
図2 鏡像音源モデル (斜入射の場合)
このときの受音点Rにおける音圧および法線方向粒子速度は次の式で表されます。
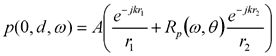 (9)
(9)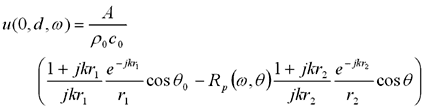 (10)
(10)このときのノーマル比音響インピーダンスは、
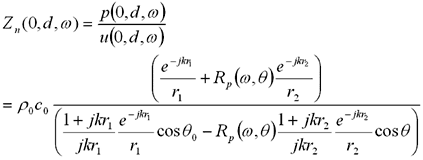 (11)
(11)よって、上記インピーダンスが得られれば音圧反射係数を求めることができます。
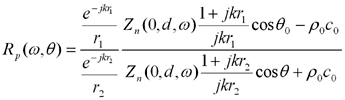 (12)
(12)3. 自由音場法の実測例
それでは本手法を用いた測定例をご紹介いたします10),11)。測定したのは2種類の材料(グラスウール、吸音性ウレタンフォーム)です。測定ブロック図を図3に示します。半無響室の床のほぼ一面に試料を敷き詰め、音源信号には正弦波スウィープ信号を用いて測定しました。また、室内の不要な反射音を取り除くためにRaised-cosine windowによる時間窓をかけた音圧および粒子速度のインパルス応答をFFTして比音響インピーダンスを求めました。その比音響インピーダンスに2.2で説明したSurface impedance法で音圧反射率を求めて吸音率を算出しました。
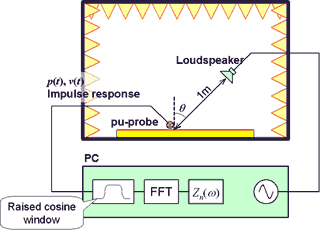
図3 自由音場法による吸音率測定のセットアップ
垂直入射条件での吸音率の測定結果をそれぞれ図4に示します。自由音場法での測定結果との比較として、音響管での測定結果とBiot-Allardモデル7)での計算結果をあわせて示しています。Biot-Allardモデルでの計算には伝達マトリクス法12)を用いました。そのときの計算に使用した材料パラメータは表1のとおりです。
グラスウールの結果は3者とも比較的良く一致しているのがわかります。グラスウールのような材料は空気伝搬音(材料中の空隙を伝搬する音)の減衰のみにより吸音性能が表せるので、音響管内における試料の大きさや拘束条件による固体伝搬音の影響はほとんど無いと考えられます。したがって、音響管での測定結果と自由音場法の測定結果は同じような結果が得られるはずです。図4に示す結果は、この考察を反映するものであり、Biot-Allardモデルの計算結果とも概ね一致しています。この結果からわかるとおり、グラスウールのような材料であれば、自由音場法の妥当性の検証の比較対象として音響管の測定結果を用いることができるといえます。ところが吸音性ウレタンフォームの結果は2つの実測と計算結果にそれぞれ多少のずれがみられます。ここで着目すべきは吸音のピーク周波数です。Biot-Allardモデルの計算結果と自由音場法の測定結果は振幅に若干ずれがみられるもののピーク周波数はほぼ一致しているのに対し、音響管による測定結果の吸音率のピーク周波数は高めにシフトしています。これは吸音性ウレタンフォームの吸音メカニズムによるものと考えられます。つまり吸音が単に空気伝搬音の減衰だけでなく、固体伝搬音における損失も含んでおり、切り出したサンプルが周囲を音響管に拘束されているために、見掛けの弾性率が大きくなったためであろうと考えられます。
表1 Biot-Allardモデルで使用した材料パラメータ
| Material | Glass wool 96K (25t) |
Urethane foam (50t) |
| Flow resistivity[Ns/m4] | 55000 | 100000 |
| Porosity | 0.96 | 0.99 |
| Tortuosity | 1.07 | 1.6 |
| Viscous char. length [m] | 5*10-5 | 1*10-5 |
| Thermal char. length [m] | 1*10-4 | 3*10-5 |
| Density [kg/m3] | 96 | 40 |
| Shear modulus [N/㎡] | 1*105 | 2.5*104 |
| Loss factor | 0.25 | 0.15 |
| Poissons ratio | 0 | 0.1 |
(a)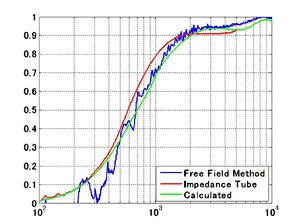 (b)
(b)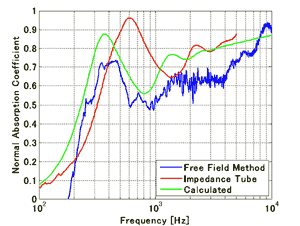
図4 垂直入射吸音率の測定結果とBiot-Allard モデルによる計算結果の比較
青: 自由音場法、赤: 音響管による方法、緑: Biot-Allardモデル
(a) グラスウール、 (b) 吸音性ウレタンフォーム.
続いて斜め入射条件での測定結果を図5、図6に示します。測定結果との比較として、Biot-Allardモデルでの計算結果をあわせて示します。グラスウール、吸音性ウレタンフォームともに自由音場法の測定結果と計算結果は比較的良く一致していることがわかります。このように、斜め入射条件での吸音率の評価ができることも自由音場法の一つの特徴です。
(a)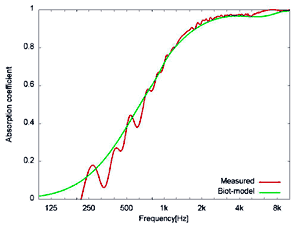 (b)
(b)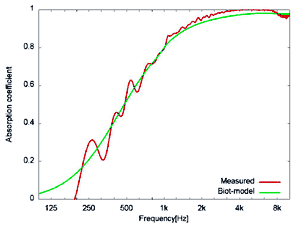
図5 グラスウールの斜入射吸音率
赤: 測定結果、 緑: Biot-Allardモデルによる計算結果
(a) 入射角度30°、 (b) 入射角度60°
(a)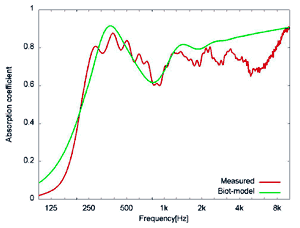 (b)
(b)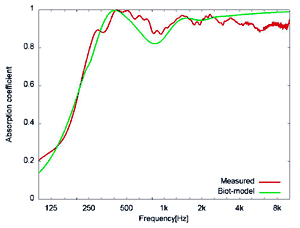
図6 吸音性ウレタンフォームの斜入射吸音率
赤: 測定結果、 緑: Biot-Allardモデルによる計算結果
(a) 入射角度30°、 (b) 入射角度60°
別の実測例として、以前いすゞ中央研究所様から委託業務として測定させていただいたデータの一部を図7に示します。測定試料は先にご紹介したものと同じグラスウールです。これを半無響室床面一面に敷き詰めたときの垂直入射条件において、音源の高さ違いを2.1の平面波近似と2.2のSurface impedance法の2つのモデルで求めた測定結果と音響管での測定結果を比較したものです。音源高さが1.5mの場合は平面波近似とSurface impedance法はほぼ同じ結果が得られ、音響管での測定結果ともほぼ一致しています。一方、音源高さ0.25mの場合、平面波近似では音響管のデータよりも吸音率が高めになり、逆にSurface impedance法では音響管のデータよりも吸音率が低めになっています。これは、0.25mという高さでは平面波入射という仮定が成り立たないためです。このような場合は、試料に球面波が入射するという条件をより厳密に解いた結果13)をもとに反射係数を計算しなければなりません。実際にこの手法を用いている文献14)もあり、弊社でも球面波音場におけるモデルを用い、音源が近い場合の測定精度の向上に努めています。
(a)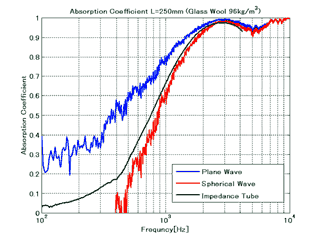 (b)
(b)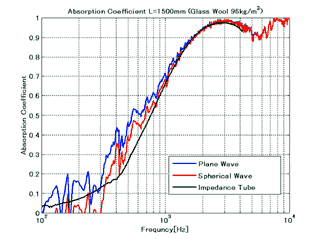
図7 グラスウールの垂直入射吸音率
青: 平面波入射を仮定した測定、 赤: Surface impedance法による測定、 黒: 音響管による測定
(a) 音源の高さ0.25mの場合、 (b) 同1.5mの場合
4. おわりに
これまであまり耳慣れない自由音場法という測定方法をご紹介させていただき、いくつかの実測例を示しながらその有用性を説明させていただきました。今後はより測定精度を高めるのと同時に、音響管では評価が難しいサンプルへの適用を行い、多くのお客様にご利用いただけるようにしたいと思います。
謝辞
図7に掲載した自由音場法に関する測定業務委託いただいたいすゞ中央研究所様に感謝申し上げます。
参考文献
- ISO10534-2 Acoustics -- Determination of sound absorption coefficient and impedance in impedance tubes -- Part 2: Transfer-function method.
- 伊積, 岩瀬, ”音響管を用いた伝搬定数の簡易化方法について”, 音講論,1993.3.
- 岩瀬他, ”音響管計測における多孔質材料の共振現象の軽減方法について”, 音講論,1996.3,805-806.
- 山口他, ”各種多孔質材料の音響特性(第7報)”,音講論, 1994.10,893-894.
- J. F. Allard and Benita Sieben, “Measurement of acoustic impedance in a free field with two microphones and a spectrum analyzer” J. Acoust. Soc. Am. 77, 1617-1618 (1985).
- 日本音響エンジニアリング 技術ニュース22号
- J. F. Allard “Propagation of Sound in Porous Media : Modeling Sound Absorbing Materials” Elsevier Applied Science.
- 日本音響エンジニアリング 技術ニュース25号
- I. Rudnick, “The propagation of an acoustic wave along a boundary,” J. Acoust. Soc. Am. 19, 348-356 ( 1947).
- 金他, ” PU-プローブを用いた自由音場法による音響材料の吸音率測定-その1 垂直入射吸音率を用いた測定方法の検討-”,音講論, 2007.9,1027-1028.
- 廣澤他, ” PU-プローブを用いた自由音場法による音響材料の吸音率測定-その2-斜入射吸音率の測定結果と伝達マトリックス法による計算結果の比較-”,音講論, 2007.9,1029-1030.
- B. Brouard, D. Lafarge and J. -F. Allard, ”A general method of modeling sound propagation in layered media”, J. Sound Vib. 183, 129-142 (1995)
- M. A. Nobile and S. I. Hayek, “Acoustic propagation over an impedance plane,” J. Acoust. Soc. Am. 78, 1325-1336 (1985).
- J. F. Allard and Y. Champoux, “In situ two-microphone technique for the measurement of the acoustic surface impedance of materials,” Noise Control Eng. J. 32, 15-23 (1989).




