技術ニュース
冊子版アーカイブ

営業部 中野 徹
技術部 忠平 好生

1. はじめに

無響室には匂いがあります。またまた変な話から始まりますが、以前、無響室には顔があると書いた事があります。どんな顔であれ出来上がった無響室はきれいなものです。ところで匂いがある事にお気付きでしょうか？ちょっと赤ちゃんを思い出して下さい。赤ちゃんには匂いがしませんか？そうです。乳臭くありませんか？そうなんです。無響室にも赤ちゃんと同じく生まれたては匂いがあるのです。残念ながら、人間の様な乳臭さではなく、フェノールの匂いがするのです。
ほとんどの無響室は、吸音層にグラスウールを使っています。また、グラスウールの色はほとんどが黄色です。何故、黄色でしょうか。
グラスウールそのものの素材はガラスであり、白色なのです。ある長さを持って高温で炉から吹き出されてきます。このままではファファの状態であり、とても製品として使いものになりません。ある形状にするためには、接着剤で固める必要があるのです。そうです。この接着剤がフェノールなのです。グラスウールが黄色いのはこのフェノールによるものです。このフェノールの匂いは、アルコールの甘味をとった匂いとでも言ったらよいでしょうか。ちょっとした刺激臭です。
時には、目がチカチカする事もあります。経験のある方なら、無響室に入った瞬間、無響室が古い物なのか、新しい物なのか、匂いでも判断できるでしょう。無響室を新設された時には、空調又は換気を1ヶ月位行う事をお奨めします。2～3週間で臭いは取れます。また、気になるようであれば、大型脱臭材の併用が有効です。
以前、NOEニュースで無響室の設計について、Vol.2では"無響室とは"、Vol.8では"無響室の設計は全体レイアウトである"と述べてきました。また、厚顔無恥にも、音響設計は音響専門者へとも述べてしまいました。
余り能書きばかり述べても、本当に大丈夫かなあ～と不安に思われてしまいそうなので、今回は音響設計の内、特に重要な音場設計について当社の考え方を述べる事にしました。
今回は数式が少し出てきます。（分かりやすくするため、出来るだけ簡単な数式とし文章で説明するつもりです。）頭の痛くなられた方は、次項の三角関係だけでも理解して頂ければ幸いです。また、理論や数式に慣れておられる方、当社はまだまだ力不足です。どうか、不足の点は、御叱責、御教授の程よろしく御願い致します。

2. 無響室音場設計の三角関係 （L、ro、IRIの関係）

音響設計の詳細に入る前に、先ず基本となる三角関係にふれておきたいと思います。音場設計には3つの要素があり各々が関連しているのです。（図1参照）
3要素とは、

1. 無響室の大きさ L
   音源から受音点に向かった時、音源から吸音面に至るまでの距離
2. 音源・受音点間の距離 ro
   必要とする自由音場の距離と考えられ、逆自乗則成立範囲とも言えるでしょう。
3. 吸音層の音圧反射率 IRI
   注：この音圧反射率（IRI）と吸音率（α）の関係は次式で表されます。

α = 1 - IRI2

であり、この1～3は密接に関連しているのです。
3点を同時に指定できないものだと理解して下さい。
残念ながら、部屋の大きさと逆自乗則成立範囲と吸音層音圧反射率の3点を同時に決定することは出来ないのです。逆に言えば、3点の内、2点が決定され残りの1点を決めるのが音場設計とも言えるでしょう。

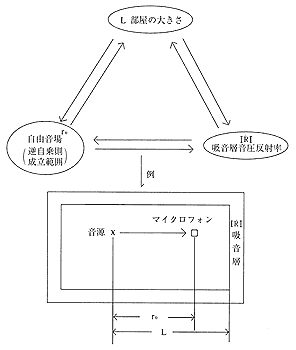
図1 音場設計の3要素

もう少し、L、ro、IRIについてふれておきましょう。
Lは、大きく取れば取る程2、3の性能を緩くすることになります。そうです、"大きい事はよい事だ"に通じます。このことは直感的に御理解頂けるでしょう。大きな空間さえあれば、吸音層の如何にかかわらず小さな自由音場は得られるものなのです。かといって、小さな時計等の音を計測するのに数Mもの大きい部屋を考える人はいないでしょう。2とも絡みますが、Lは測定対象物の大きさに支配されるものだと理解して下さい。
また、2、3が決定された場合、前記の如くは、音源から受音点に向かった時、音源・吸音層間の距離を表しますので、逆に音源位置をどこにすれば良いかという問題に置き換えられます。これも音場設計の一つです。
ちなみに受音点から吸音面までの距離は、測定下限周波数の1/4波長か1m
（但し、補機類等の制限がないものとします）のいずれか大きい方が一つの目安になります。
次にroについてですが、これは規格等で指定される場合が多いのです。ISOでは音源中心から測定対象物最大寸法（注として、対角線の長さを忘れないで下さい。）の2倍となりますし、JISの一部では、音源機側1m点と言うように指定されています。oroの決定には、規格に十分注意することが必要となります。
最後にIRIですが..難しい問題があります。IRIが小さいほど良いに決まっています。理想は当然0（吸音率100%）なのですが、これは現時点では不可能です。
将来、アクティブコントロールの技術が発達し、全面スピーカー又は有限の平板で囲われた無響室が存在するかも..。今はDSPの開発も進み相当対応スピードが上がってきましたが、過渡状態を考えますとどうなるんでしょう。楽しみですねえ～IRI＝0が無理とすれば、当面は0.1（吸音楔であれば遮断周波数となります）が、一つの目安になります。
難しい問題があると述べましたが、その一つは測定下限周波数との絡みです。 吸音楔の場合、下限周波数（以下ｆcと省略します。通常これは音圧反射率が0.1となる周波数をさし、遮断周波、カットオフ周波数とも言われています）を63Hzとすれば楔の長さは1m程必要となりますし、一般的な125Hzとしても600mm必要となります。ちなみに、日本にある最長の楔は残念ながら当社にはありませんが、長さ約1800mmｆc≒38Hzのものがあります。
楔を長くすることは、施工費が高くなると同時に1のLにも絡み、部屋の大きさは即コストに反映され、高価なものになってしまいます。大変ですねえ～
しかも、ｆcはだんだん低くなる傾向にあります。これはVol.2で述べた通りです。困りますねえ～しかし必要ですねえ～難しい問題になりそうです。（予算のある方はいいですねえ～羨ましい限りです。）
この問題は次の問題にも絡みます。
1でも述べましたが、部屋を大きく大きくすれば、またroが小さければ小さい程、前記問題も少し楽なのですが。
当社は昔から（昔と言っても20年迄は至っていませんが）ISOに従った音場設計を心掛けて来ました。ISOに従いますと"吸音層には測定下限周波数を遮断周波数とする吸音楔を用いなさい"とあります。従って、音場設計によりLを大きくとりIRIが0.2でroが十分確保できてもダメだということになります。
規格は規格なので困っています。もっともこれらの問題は無響室を設計される方の考え方に支配されます。無響室の目的によって多少無響室のスタイルが異なってくるでしょう。これも無響室の顔と言えるでしょう。
以上、いずれが必要かという問題はさておき（いずれも重要事項なのですが）L、ro、IRIについて少しくどく述べました。要は三角関係が存在することを理解して頂ければ幸いで、これからの数式の理解に役立つものと思います。

3. 自由音場の設計

2で述べましたL、ro、IRIの三角関係を解きほぐすため、この三角関係を示す式を考え方と同時に表していきましょう。
これは、

1. L、roが決まっている時、IRIの決定
2. IRI 〃ro〃
3. IRI 〃L〃
4. L、ro、IRI〃音源位置の決定

をする方法になります。

3-1 拡散音場の考え方

これは少し古い方法で、当社も20年前まで行っていた方法です。
実際は、無響室はほとんどの音を吸収してしまいますので、拡散音場とは言えないでしょう。但し、従来使用されていた考え方（三角関係の表し方）なので、紹介しておきます。これは、無響室以外の場合にも、数多く使用されていますので参考になるでしょう。
今、無響室内に理想的点音源（考え方としては、ある音響出力を持ち、かつ大きさがなく、指向性がない音源とします）が置かれた時、この音源からm離れた受音点における音圧は次式で表されます。

1-1の式

ここに
SPL拡：音場からm離れた音圧であり、直接音以外に反射音も含んでいるためとします。
SWL:音源の音響出力でパワーレベルを表します。
r:音源と受音点の距離
R:室定数と呼ばれるもので、次式で表されます。

1-2の式

a:室を取りまく表面材の平均吸音率 S:室の表面積 1-1式の（）内は、1/4πr2が直接音の減衰を示し、4/R拡散音の大きさを示します。 グラフで表示しますと、図2のようなグラフになります。

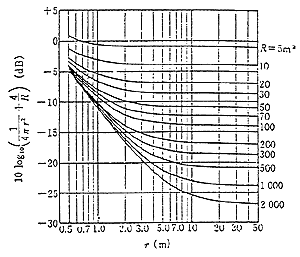
図2 拡散音場における音圧距離減衰特性（Q=1の場合）

よく見られるグラフだと思います。
当然ながら、部屋の吸音力が増せば、SPL拡は距離と共に理想的（-6dB／倍距離）に減衰します。
1-2式において、 sが一定ならば、āが大きくなればなるほどRが大きくなり、1-1式の4/Rの項が無視出来るオーダーになることを示します。これは、とりもなおさず無響室を作ることになるのです。
次に、直接音だけを考えてみましょう。1-1式において、4/Rが無いことになりますので、直接音のみの音圧レベルをSPL直としますと、SPL直は次式で示されます。

1-3の式

これも、よく見る式ではありませんか？
半自由空間の場合は、指向係数が入るため1-3式は

SPLの式

となり、最後の定数が変わります。これは、直接音の他、床なり、壁面なり、1面からの反射が加わり、音圧レベルが3dB上昇することを示します。
さて、元に戻り、無響室では1-3式で示される関係が欲しいのです。つまり、実測できるSPL直とrからを求めることが当面の目的となります。
ところが実際は、1-1式で示される音場になるわけですから、1-1式から1-3式を引いた音圧レベル差が理論値（逆自乗則）からの誤差を表すことになります。この音圧レベル差をΔSPLとすれば、1-1式から1-3式を引き算し

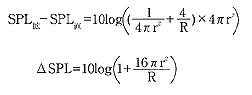1-4の式

と表されます。
今、このを許容誤差δｄBとすれば、

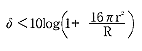1-5の式

となれば良い訳ですから、rを逆自乗則成立範囲（自由音場）とすれば、1-5式より、

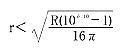1-6の式

となり、更に1－2式を代入すれば、

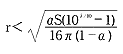1-7の式

となります。
1-7式から分かることは、aを大きくし、Sを大きく取れば、rが大きくなります。これは当然のことなのですが、吸音率の大きい吸音層（aを大きくすること）を用い室を大きく（Sを大きくすること）することに外なりません。
但し、この式とは前記のLの項がありません。室の大きさを決定するのはちょっと難しいとは思いませんか？
当社では、現在この考え方では無響室の設計を行っておりません。その理由を少しふれておきます。

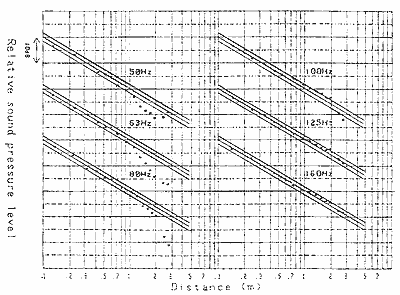
図3 実測例

1 実測値と違いすぎる?

当社は、完成された無響室の性能測定を数多くやってまいりました。その中で、拡散理論ではどうしても説明できない測定値例が数多く出てきました。
もう一度、1-1式、1-3式を見てみましょう。実測可能なSPL拡はSPL直より必ず大きな値となります。当然、SPL拡はSPL直に拡散音（吸音層からの反射音）のエネルギーを加えたものですから、SPL拡＜SPL直とはなり得ないものです。ところが、実測例は、図3に示す実測例が多いのです。
しかも、吸音率の低い（反射音が多くなります）周波数において多いのです。反射音が多いにもかかわらず、音の減衰が大きいのです。一時は困りました。どう説明したらよいのでしょう。悩んだ結果、次項で述べる方法で検討したところ、光が見えてきました。詳細は次項に譲りますが、結論は、拡散音ではなく吸音層から反射した音の位相干渉だったのです。

2．半無響室は大きくなければダメ？

20年前から半無響室が数多く作られてきました。1-7式をもう一度見てみましょう。
半無響室の場合、r（逆自乗則成立範囲）を大きくするには、反射面の吸音率が限りなく0に近いため、を大きくするしかありません。（aを大きくするには、床面以外の吸音層に大きな負担を掛けることになります）本当でしょうか。この疑問にも困ってしまいました。
半無響室の逆自乗則特性（音圧距離減衰特性）をどう考えたらいいのでしょう。音源が反射面にある場合は、半自由空間ですから考え易いのですが、音源が反射面＋αにある場合はどうしましょう。ホワイトノイズのように全帯域の周波数成分を含んだものであれば、単純にエネルギー合成だけで済みそうですが、純音、ないし狭帯域ノイズの時はどうなるのでしょう。実測したところ、直接音と反射面からの反射音が干渉し、複雑な音圧距離減衰特性を示しました。とても吸音層からの反射が云々と言えるような状態ではありませんでした。参考例を図 4に示しておきます。

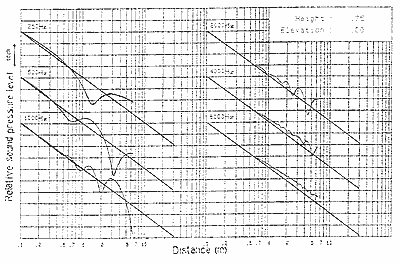
図4 完全反射面上における音圧距離減衰特性

図4は床面を完全反射面とし、床上に0.75m点における音圧距離減衰特性を算出したものです。

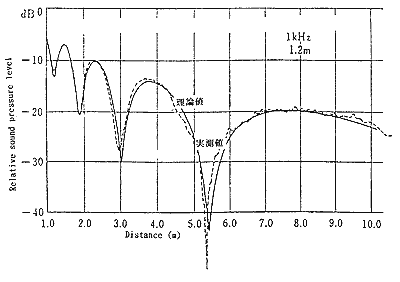
図5-1 半自由空間における音圧距離減衰特性（1）

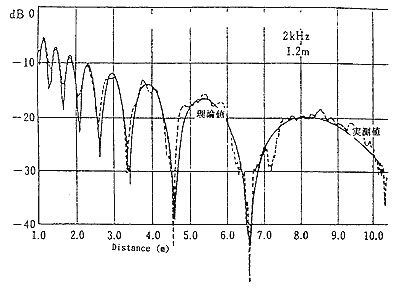
図5-2 半自由空間における音圧距離減衰特性（2）

図5は実測例であり、床上1.2mでマイクロフォントラバースを用いて得うれたものであり、距離はリニアー軸となってます。
半無響室の音場設計はさておき（考え方としては、反射面を鏡面と考え、鏡面で折り返した倍の大きさを持つ無響室として取り扱うことにしています。）
前記の直接音と反射面からの反射音の干渉を検討した事が見事に役立ちました。即、反射面を吸音面として考えてみたのです。それが次に示す考え方に発展しました。

3-2 位相を考慮した幾何音響の考え方

当社は3-1の後半で述べましたように、拡散音場の考え方では説明しきれない現象にたくさんぶつかってきました。

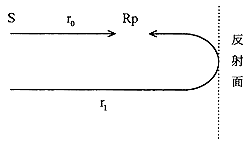
図6 音場モデル

これらの問題を考えている内に、以下に述べる考え方でいくつかの問題点を解明できるようになってきました。まだまだ問題点はありますが、この考え方で音場予測計算をしたところ、計算値と実測値がよく一致しました。従いまして、現在当社ではこの方法で基本的音場設計を行っても支障はないと判断し、この考え方を採用しています。ここでは、基本的考え方を紹介することに致しましょう。
3-1と同様、無響室内に点音源（S）を設置する場合を考えてみましょう。話を簡単にするため、音源から放射される音は単一周波数（純音）とし、吸音面（反射面）は音源から受音点（Rp）に向かった時の一面のみとします。
Rpにおける音圧Pは、直接音P1と吸音面からの反射音P2を合成すれば求まります。吸音面の反射係数をRとし各々の音圧を示すと

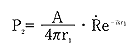2-1の式2-2の式2-3の式2-4の式

となります。ここに
A：音圧振巾
ro：S，RP間の距離
k：波長定数
r1：Sから反射面を経てRPにいたる距離
IRI：音圧反射率
φ：位相角（反射の際に起こる位相のズレ）
従って、Pは次式で表されます。

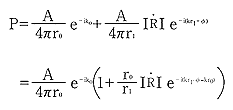2-5の式

一方、測定可能量となる音圧レベルと音圧の関係は

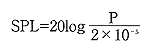2-6の式

と表されますから、P点における音圧レベルを、SPL直+反直接音の音圧レベルをSPL直としますと、2-6式より

2-7の式

となり、この音圧レベル差ΔSPLが逆自乗則からズレを示すことになります。2-2式、2-5式よりを求めます。

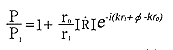ΔSPLの式

オイラーの公式を用い

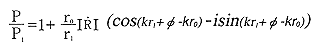オイラーの公式ΔSPLの式

と表されますので

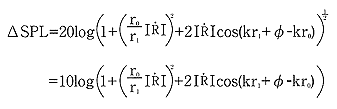を求めると2－7式より2-8の式

これが、三角関係を表す式となります。
音源から図6の反射面までの距離をLとすれば

r1＝2L－r0

となりますから、2-8式はL、ro、IRIをすべて含んだ式となります。 また、△SPLを算出する際、COS項を含んでおりますのでroを変化させれば、音圧も直線ではなく、波打つことになり3-1で述べた怪奇現象も説明がつきます。 実際の音場設計には三次反射までを考えた式を用いて計算しています。例えば、三次反射とは図7に示す反射であり、経路的には平・断を含めるとかなりの数となります。参考に計算値と測定値を比較してみましょう。図8は計算値であり、図9は実測値です。

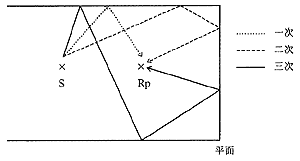
図7 反射の例
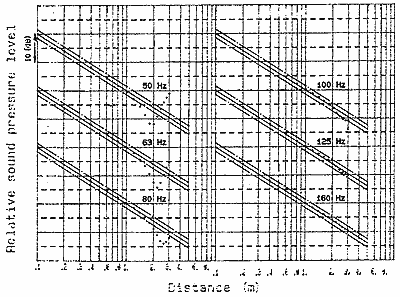
図8 完全無響室内音圧距離減衰特性予測値
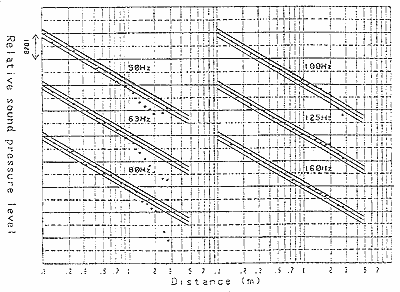
図9 図8の実測値

計算値と実測値はよく一致しており、低周波域で拡散音場の考え方では説明出来なかった現象も見事にシミュレート出来たことになります。
現在、ほとんどの無響室は上記考え方を拡張した計算ソフトでコンピューター処理により音場予測が可能であり、計算の手段として利用しています。今のところ、計算値と実測値はよく一致しており、大きな問題はないと判断しています。
音場設計の方法としては、有効な手段であることが多少ご理解頂けましたでしょうか。短時間で結果をすぐ打ち出せますので、いつでも安心してご利用下さい。
さて、能書きはさておき"大きな問題はない"と書きましたが、これはとりもなおさず小さな問題がまだ残っているということです。小さな問題（本当は重要なことなのですが）に少しふれておきます。

1 IRIの問題

この幾何音響の考え方で用いている音圧反射率は実は音が吸音層に垂直に入射した時のデータを用いているのです。実際の音場を考えますと、音が吸音層に垂直に入射する場合は少なく、斜めに入射する場合が多いのです。
残念ながら、斜入射に対するデータの蓄積は当社にはほとんどありません。データを得るのが非常に難しくコストがかかります。悲しいかな当社はまだまだ力不足です。もっとも一般の吸音材についてもほとんどデータがないのが実情だと思いますが..。
実は、この音圧反射率の他に反射の際に起こる位相のズレの問題があります。完全反射、完全吸音でない限り、音が吸音材に当たった時、音は位相が少しズレて反射してきます。斜入射と絡むとほんとうに難しい問題となります。当社では経験値を採用しています。これも今後のデータ蓄積が課題です。

従って、音場の厳密予測は出来ないのです。ですが、予測値と実測値がそこそこ（±1dB以内の誤差範囲ですが、距離減衰特性の山・谷の位置が微妙に違っています）一致しており、実用上問題無いと判断しています。
今後、斜入射のデータが蓄積されてくれば解決できるでしょう。但し、無響室において現在以上の厳密解を求める必要があるかどうかは疑問です。現状で十分対応出来ているのですから..少し甘いですか？

2 無響室は立方体もしくは直方体のみ?

情けない話ですが、現在当社でシミュレートできる無響室は立方体、もしくは直方体のみで、しかも全面同一の吸音材が用いられているという条件がつきます。
但し、ほとんどの無響室は、シミュレート可能です。
大きな反射面がある場合、吸音面の特性が異なる場合、今のところ計算（コンピューター入力の方法）テクニックでそこそこ対応しているのですが・・・
特に困るのは建築的に無響室の大きさが制限される場合です。大きな柱や梁があり無響室内に無視できない程大きな反射物がある場合です。残念ながら、この方法はシミュレートできないのです。これらの問題は次に述べる方法で現在行っております。
但し、前記の如く特殊な場合は、数少ないですし、無響室を計画される方でわざわざ反射物が出来るような場所は選定しないでしょう。
もし、どうしても無響室に制限がつけられる場合は、次の方法を現在応用しています。

3-3 波動音響理論に基づく考え方(境界要素法の利用)

この方法は、現在当社で行っている最新の方法です。但し、ほとんどの場合3-2の方法で音場設計が行えますので、これは特殊な場合と考えてください。
この理論は、当社技術部の忠平により提案された境界要素法による音場解析の方法として境界積分方程式を用いたものです。詳しくは前号の技術ニュースを参照してください。
今回はこの方法を無響室に適用したときの考え方、シミュレーションの方法、実測値との比較を実例と共に紹介してみます。

図10 無響室の形状及び寸法と吸音材の配置（寸法の単位は[m]）

最初に御断りしておきますが、これは特殊な場合にのみ適用しており、通常は3-2の方法で行っております。
(実は、社内でもまだ汎用化されておりません。誰でもすぐにホイホイという訳にはいかないのです。コンピュータ入力に時間と労力がかなりかかりますし、演算にもコンピュータがフル稼働となります。厳密解を得るにはもう少し時間をください。この考え方の利用範囲は広く、無響室以外にも応用しているところです。)
前にも触れましたが、3-2の方法では無響室の形状が立方体か直方体であり、しかも全面同一の吸音材が用いられているという条件が必要になります。一般には、無響室を計画する際にこの条件が満たされないことはほとんどありません。しかし、既存の建て屋の中に無響室を設けたい場合、即ち改装工事を行う場合には、躯体の構造によって建築的な制限が生じることがあり、上記の条件から外れてしまうために3-2の方法での音場予測ができないことがあります。ところが困ったことに、このような場合にこそシミュレーションによって音場を予測して、測定に使用できる範囲や周波数限界を把握したいのです。そこで当社では、条件設定に制限がなく、より厳密解に近い結果を得られる境界要素法に独自の改良を加えた手法を用いてこのような問題に対処しています。
一般に音響問題を境界要素法で解く場合、Greenの定理(体積積分を面積積分に変換する公式)と波動方程式を連立させて境界積分方程式を導きます。説明のため、この方法の基礎となる積分方程式を紹介します。

3-1の式

ここで、φは速度ポテンシャル(音圧と考えてもらっても結構です)、Pは音場内の受音点座標、Qは音場を取り囲む境界上の点の座標、ｄは音場内に存在する唯一の点音源と受音点Pの間の距離、rは受音点Pと境界上の点Qの間の距離、nは点Qにおける内向き法線ベクトル、は波数(角周波数/音速)を表します。ご覧いただければわかると思いますが、3-2までで引用してきました数式に比べるとかなり複雑な計算が必要になります。
この式を物理的なイメージと照らし合せて見ますと、右辺の第1項は音源からの直接音に対応し、第2項の積分は境界からの寄与(反射音のようなもの)に対応していることがわかります。つまり、受音点の音場が音源からの直接音と境界からの反射音の和で求められると考えればわかりやすいと思います。
この境界積分方程式を用いた方法は既に実用化されており、かなり高価ですが汎用の計算プログラムが市場に出回っています(残念ながら日本製ではないのですが...)。というように、今やメジャーな手法となっていますが、吸音性能の高い材料を使用した空間（その最たるものが無響室や半無響室になります）の音場予測を行うと、実測との比較において大きな差が生じることが当社の研究でわかりました。私共はこの原因が境界での吸音の取り扱い方にあることを突き止め、これを改良する方法を提案し、現在その検証作業を進めています。

• 
• 

(a)平面(z=1.85[m]内の受音点位置と計算結果)

• 
• 

(b)断面(y=1.75[m]内の受音点位置と計算結果)

図11 定常音圧レベル分布（単位は[dB]）（音源からの距離0.1[m]の位置を0[dB]とした相対レベル[dB]）

これについての詳細な説明はかなり専門的な話になってしまいますので、今回は割愛させていただきます。また、日を改めて御紹介したいと思っております。

さて、前号ではこの方法による過渡音場の計算手法について御紹介しましたが、今回は定常音場の計算手順を簡単に説明します。
計算に必要なパラメータとしては、上記の数式を見てわかるように主として室の形状、壁や床などの各面の境界条件(複素音圧反射係数)、音源の位置と駆動周波数、受音点の位置です。まずコンピュータ上での数値計算を可能にするためには、上式の積分を離散化する(∫をΣで近似する)必要があります。そのために境界を駆動周波数の波長に応じた大きさの面積要素に分割し、各要素内の音圧は一定と考えて、要素内の音場を未知数とした一次方程式を組み立てます。ここで、左辺のφを右辺のそれと同様に境界要素内の音場を表す未知数と考えると、この一次方程式が要素の数だけ作れることになります。つまり、連立一次方程式になるわけです。これをコンピュータで解くと各境界要素上の定常応答が求められます。そして得られた境界上の応答から室内の各受音点での定常応答が計算できるという次第です。
この方法の問題点は連立一次方程式を解くところにあります。一般に境界を分割する要素の大きさは、その最大寸法を波長の1/4から1/5以下にする必要があると言われています。例えば、表面積が100m2の室の1kHzの応答を計算したい場合、要素の最大寸法を340/1000/5=0.068mとするとその面積が約0.005m2となりますので、100/0.005=20000個の要素が必要になります。つまり二万元連立一次方程式を解かねばならないことになり、コンピュータの能力如何では計算不能となってしまう場合もあります。まあ数年後にはコンピュータの性能が向上して問題ではなくなる可能性もありますが...。
以上の問題もありまして、現在当社ではこの方法を汎用的に音響設計業務に活用している状況ではありません。必要に応じて手作業でデータ入力、計算実行、レポーティングをこなしている状態です。
それでは、計算例を御紹介しましょう。建築上の物理的な問題により、室内に地中梁が突出しており、壁面の一部に吸音楔を取り付けることができない無響室を計画するにあたり、その性能を調査する目的で定常音圧レベル分布を予測計算した例です。幸いなことにこの無響室の施工が完了し、検収測定(逆自乗特性の測定)の結果が手に入りましたので、予測値と実測値との比較も御紹介します。
図10に計算対象とした無響室を示します。ご覧のとおり、床中央に梁が突出し、二つの壁面の下側に吸音楔を取り付けることのできない領域が生じています。この影響をもろに受けてしまうのは、測定下限周波数に相当する125Hz帯域でしょう。そこで、この周波数帯域の定常音圧レベル分布と最も厳しいと思われる斜め下方への逆自乗特性をコンピュータで予測し、実際の使用に耐えられるかどうかの調査を行いました。シミュレーションでは、点音源を純音で定常駆動した場合の結果が得られるのですが、より実際の条件に近付けるために1/3オクターブバンドノイズで駆動した場合を想定し、バンドに含まれる対数軸上で等間隔に選んだ11の駆動周波数での定常応答を合成して結果を算出しました。
各計算条件は以下に示すとおりです。

(1)境界要素分割:	706個の四角形要素
(2)音源位置:	図10に示す位置
(3)駆動周波数:	111.362,113.965,116.629,119.355,122.145,125,127. 922,130.912,133.972,137.103,140.308Hzの11種の結果を合成
(4)吸音材の複素音圧反射係数:	(125Hzの場合)
吸音材 振幅 位相[rad] 吸音楔(600mm) 0.08 0.325 吸音楔(450mm) 0.35 0.244 グラスウール(200mm,32kg/m3) 0.83 0.108 グラスウール(50mm,32kg/m3) 0.92 0.027 吸音なし 1.00 0.000

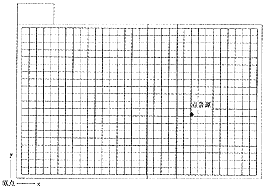
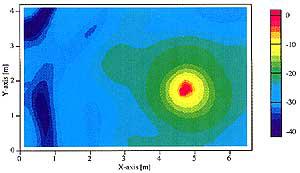
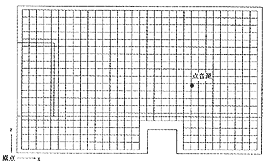
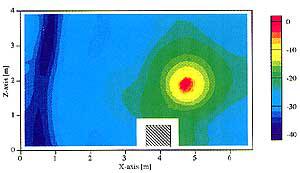
まず、図11に定常音圧レベル分布の計算結果を示します。図11のように音源を含んだ平面及び断面内に20cmの等間隔に受音点を設置しました。450mmの吸音楔を取り付けた面からの反射による定在波の影響や、床中央の梁による音波の干渉が生じていることが確認できます。

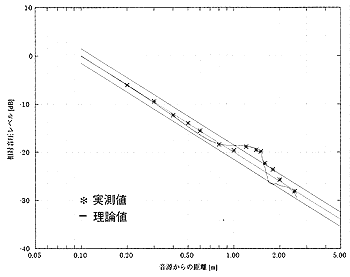
図12 逆自乗特性（音源からx軸負方向に対して仰角45度方向）

次に、この音場の乱れが規格の許容差に含まれるかどうかを調査するために、最も厳しいと思われる音源からx軸負方向に対して仰角-45°方向の逆自乗特性を計算しました。結果を図12に示します。赤の線が計算結果を、水色の線が理想特性、緑の線がISO規格の許容偏差を表しています。また、検収測定の実測値を*でプロットしています。この結果から、この測定方向に関しては音源から1m以内であれば現実に使用可能であることがわかります。また実測値との比較から、計算値が非常に良く一致しています。
以上のように、これまでの理論では対応できなかった複雑な条件の無響室の音場が、ほぼ完璧に計算できるようになりましたが、まだ問題は残っています。既に問題点は述べましたが

1. IRIの問題
   これは、3-2の考え方に示した問題と同様です。
2. 計算時間の問題
   計算時間というよりも、シミュレーションの対処となる周波数の問題とも言えるでしょう。周波数が高くなると要素の数が多くなりコンピューターの容量次第ということになります。いずれは解決できる問題でしょうが..。今は250Hzが当社における計算の下限周波数となっています。

の2点が残っています。
しかし、今回示した実測例からもお分かり頂けると思いますが、十分音場予測が可能だと判断しています。
このような試みは当社が初めてであり、他社はまだ対応できないと自負しております。特殊な無響室や半無響室を計画しようと思っている方がいましたら、御気軽に声をかけてください。当社としてもこの技術の有効性を検証するために、多数の物件について音場予測を行い、その結果を活かしてさらに技術を磨いていきたいと考えております。

4. まとめ

今回は当社における音場設計の考え方を紹介させて頂きました。専門業者もそれなりに努力していることが分かって頂けましたでしょうか？未完とは言え、ほとんどの無響室の音場設計（音場シミュレーション）が行えます。

安心してお任せ下さい。また、内容について不明な点がありましたら御遠慮なくお問い合わせ下さい。
最後に御願いがあります。当社も出来るだけの努力はしていますが、まだまだ力不足です。今回述べました考え方に不足している点がまだまだ多々あることと思います。御気付きの方はどうかビシビシ御指摘下さる御願い致します。当社も頑張ります。
今回は少し長くなりましたが、無響室の設計に少しはお役に立てましたでしょうか。
皆様方のお問い合わせ、御叱責、御鞭撻をお待ち致しています。