研究開発部 鶴 秀生
1. はじめに
弊社の研究開発部においては自社テーマの研究開発や他社の研究開発の支援という意味での受託研究ならびに共同研究の業務があります。それらの研究開発の業務においては、騒音問題に関係する課題が多くあります。騒音低減をテーマとする場合、道路や鉄道などの交通機関の騒音に関する課題が多くあります。ここではそれらの課題への理論的なアプローチとしての振動数値解析手法について紹介したいと思います。
道路交通騒音や鉄道騒音の予測計算を行うとき、自動車走行によって直接放射される音や鉄道車両やレールを音源として設定することが多く、その音源から評価点に空気中を伝搬して到達する音のエネルギーを用いて音圧を予測する方法が一般的に用いられます。それらの計算には幾何音響を用いて経路探索をして、回折などの減音量を考慮する方法や境界要素法などのように、波動音響理論を用いてシミュレーションを行う方法などがあります。しかしながら高架道路や高架軌道においては車両通行や列車走行による路盤の振動、ならびにその振動から放射される騒音等も問題となります。研究開発部で行った振動数値解析の例としては、木琴の差分法による数値解析や、レールの振動の数値解析などが実績としてあります。今回はもっと大きな構造物である、高架道路や高架軌道等の構造物の振動解析を行うための数値計算手法について紹介したいと思います。そこで車両通行によって励起される振動を数値的に予測する方法の基礎理論として Mindlin 平板モデルによる振動解析と3次元固体力学の応用としての振動解析結果の比較を行うことを試みたいと思います。
最初の節では、Mindlin平板モデルの説明を行い、次の節では時間領域での解析方法についての紹介を行います。 その次の節では、3次元時間領域差分法を用いた方法による振動解析手法の説明を行います。 最後に両方の手法を用いた解析結果や計算効率の比較について紹介したいと思います。
2. Mindlin平板モデルの理論
高架道路や高架軌道などの構造物は、複数の点で支持された厚み h が場所によって変化するヤング率 E ポアソン比 ν を持つ等方的平板と近似的にみなすことができます。その場合の振動解析には2次元差分法モデルを用いることができます。そこで最初に2次元平板の振動基礎方程式について説明を行います。ここでは梁の振動数値計算でも比較的精度良く計算ができるTimoshenko梁理論と同様に、せん断変形の自由度も考慮したMindlin平板理論の説明を行います。
厚さ h の平板の曲げ弾性定数 D は
![]()
であらわすことができます。そのときの板の一般化応力 Mx, My, Mxy, Qx, Qy は微小要素の応力テンソル τ_{xx} 等を用いると
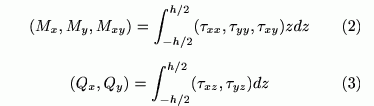
となります。これらの量は板の厚み方向について応力を積分することで定義されます。したがってある意味で平均化された量を用いて計算することになります。
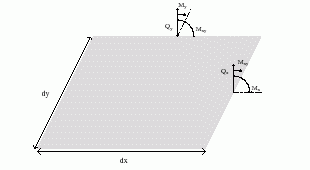
図1
ここで板の歪成分を
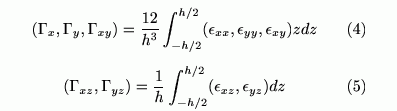
とおくことができます。振動における内部減衰の影響も考慮できるようにVoigt の粘弾性係数 η を導入すると、一般化応力はこれらの量を用いて
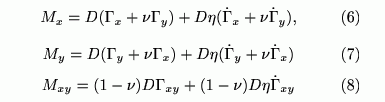
で表現することができます。
ここで G は剛性率で弾性論の理論を用いると、ヤング率 E とポワソン比 ν と G=E/(2(1+ν)) の関係があることが示せます。Mindlin平板理論においても、Timoshenko梁理論と同様に剪断係数である κ を導入して Qx, Qy とΓxz, Γyzの間に
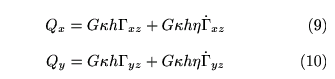
の関係を仮定します。
さて独立変数として面の法線方向の変位 w、y軸回りの回転角を ψx, x軸回りの回転角をψyとおいて変位に対して以下の仮定をおくと
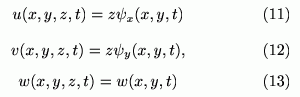
となります。なお、角度の符号が反転して定義されている場合もあります。板の歪成分をこれらの量で表すと
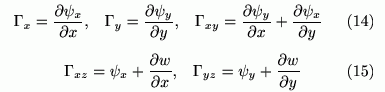
となります。粘弾性による減衰も考慮した応力--歪の関係式は
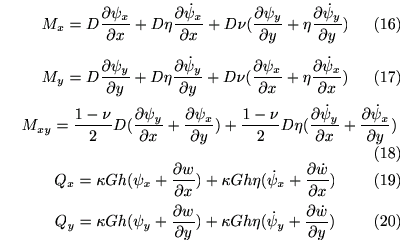
となります。これらの量を用いて表現した運動方程式は
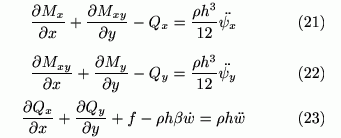
となります。ここで f は面に加わる外力で, ρは密度を意味しています。
系の時間発展方程式は
![]()
を定義すると
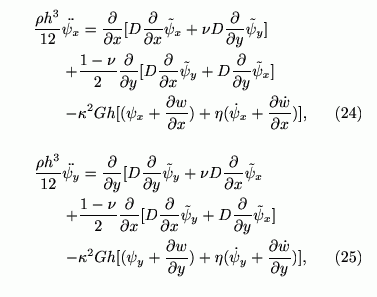
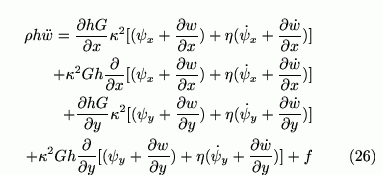
の連立偏微分方程式となります。この方程式の時間発展を解くことで、車の通過時の高架道路の振動や、列車通過時の高架軌道の振動を予測することが可能になります。
高架道路や高架軌道の側面は自由端とみなすことができるので、この節の最後に境界条件の設定方法について考えることにします。板の端での法線ベクトルを n で定義して自由端境界条件を考慮すると
![]()
の関係を満たすことがわかります。これらの方程式は
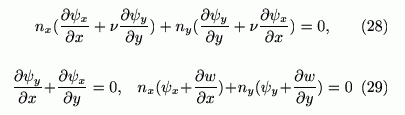
の形に変形されます。このように境界条件自体が連立微分方程式となるため、自由端の場合の解析は考慮が必要となります。
ここまでは微分方程式について議論しましたが、次の節では時間領域差分法を用いて実際に数値計算を行うときの留意点を説明します。
3. Mindlinモデルでの時間領域数値解析法
このモデルに対して、時間領域差分法による解析を行う場合には差分法による数値モデルを考える必要があります。数値的安定性を確保するためにImplicit解法により時間発展を計算する必要があります。 そうしないと、時間間隔を細かくとらないと解が発散します。
実際には以下のように方程式を減衰項を含む部分とそうでない部分に分割することから考えます。
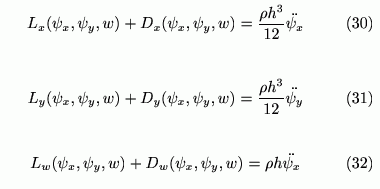
ここで Lx, Ly, Lw は減衰を含まない(時間微分を含まない)項と Dx, Dy, Dw は減衰を含む(時間微分を含む)項です。空間差分の項は更新後のタイムステップのψx, ψy, w も用い差分化します。タイムステップ n での左辺の値を引き数を省略して Lxn, Lyn, Lwn, Dxn, Dyn, Dwn で表現すると
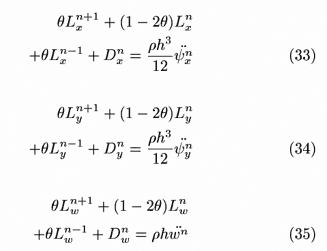
という形で微分方程式を差分化することにします。ここでθ は 0以上0.5以下の定数で θ > 0.25 で安定になります。以上の方程式で時間発展を計算するには疎行列係数を持つ連立1次方程式を解く必要があります。係数行列は ψx, ψy の行について非0成分15個、wの行について非0成分11個となるので Bi-CGstab解法によって連立1次方程式を解くことが効果的です。
最初に数値計算の精度を確かめるためにランダム加振時の振動(周辺単純支持)に対する応答を計算してみました。板の材質はコンクリートとしてサイズ: Lx × Ly = 3m ×4mで厚さ: 200mmの平板の振動解析を行いました。数値計算条件としてのメッシュ間隔は40mm × 40mm, 時間ステップは0.5msecとし, 加振力の空間分布は
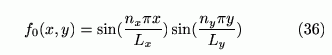
で与えました。固有周波数に対し表1の結果が得られ解析解との良好な一致を示しました。矩形の平板に関しては、かなり良好な結果が得られることがわかりました。
表1. 固有関数比較
| モード nx, ny |
解析解 Hz |
数値解 Hz |
| 1, 1 | 47.6 | 48.8 |
| 1, 2 | 136 | 131.8 |
| 2, 1 | 97.8 | 99.5 |
| 2, 2 | 184 | 184.5 |
4. 3次元差分法による振動計算
次に3次元固体力学理論を用いて平板の振動計算を行う方法について説明を行います。弾性体の変位と応力τ_{ij}はラメの定数λ,μを用いて関係付けられます。その関係式を用い、弾性体内の振動伝搬を3次元時間領域差分法を用いるための基礎方程式を示します。時間領域差分法で解析を行うには、微小要素の変位を変数として用いるのではなく、変位の時間微分である速度成分 vx, vy, vz を用いると比較的容易に定式化できます。 そのために応力成分をτ_{ij} 、弾性係数であるラメ係数をλ, μ、密度をρで表現します。ラメの弾性係数に関してはヤング率 E とポアソン比 ν と
![]()
の関係があります。この弾性係数を用いることで速度成分と応力成分の時間発展方程式は
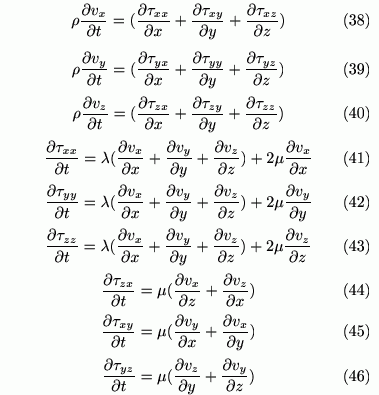
で表現できます。 応力成分と速度成分を半メッシュ空間的にずらして配置し、時間に関しても同様に半メッシュずらして時間積分を行うことで一般的なFDTDの手法を用いた数値解析が可能になります。なお空間微分に関してはコンパクト差分を用いて、微分値を評価しました。コンパクト差分とは、近似される微分値も隣接するメッシュと連立させるもので今回用いた1回微分に対するコンパクト差分式
![]()
です。これを用いることで比較的容易に、微分を高精度に差分近似することが可能になります。また差分法において時間積分を行う場合は弾性波の縦波速度 cl、横波速度 ctが
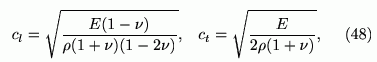
となることを考慮して、時間発展のタイムステップを決める必要があります。具体的には1タイムステップあたりに、波動が伝搬する距離が空間差分格子の間隔より小さくとる必要があります。したがって空間の格子間隔を小さくすればそれに比例して小さな時間間隔で計算する必要があるので、3次元計算の場合はそれに従って計算量が増大します。
平板の振動に関して表2の条件で計算を行いました。
表2. 数値計算条件
| 項目 | 設定値 |
| 各方向メッシュ間隔 | 20mm |
| メッシュ数 | 140×100×10 |
| 時間間隔 | 0.001msec |
| 加振条件 | 時間幅 0.5msec 三角波 |
| 周辺境界条件 | 自由端 |
| ヤング率 | 2.0×1010(Nm) |
| ポアソン比 | 0.27 |
| 密度 | 2300(kg/m3) |
加振点は面中央に設定しました。タイムステップは4000ステップほど計算を行いました。
上記の3次元差分法解析において直接得られる量は速度分布なので、速度を積分することで変位を求めることができます。加振点位置と加振点から400mm 離れた位置での変位の時刻歴をプロットしたものを図2に示します。
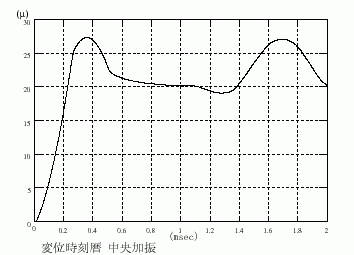
図2.1 変位時刻歴、観測点=加振点
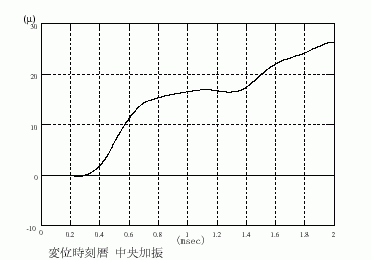
図2.2 変位時刻歴、観測点=加振点+400mm
周辺が自由であるため全体の並進移動が見られます。また加振点から離れた点においては、衝撃を加えた時刻から遅れて変位が現れることもわかります。同様の解析対象をMindlin平板モデルによる数値計算で得られた時刻歴をプロットしたものを図3に示します。
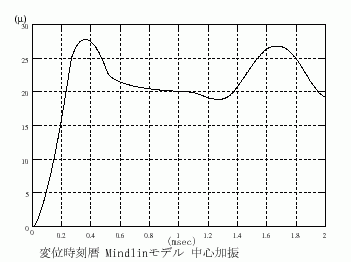
図3.1 変位時刻歴、観測点=加振点
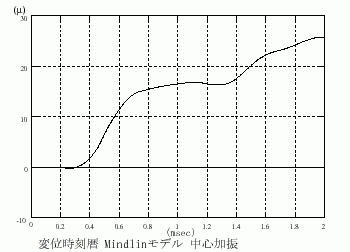
図3.2 変位時刻歴、観測点=加振点+400mm
同等の解析対象に対して、3次元差分法で計算した場合と同様の結果が得られたことがわかります。Mindlin平板モデルの場合と3次元差分法を用いた場合の計算時間の比較をATHLON64 AM2 4400+でGCC4.1.1で64Bit Linuxでコンパイルしたコードで行いました。その比較結果を表3に示しました。
表3. 計算時間比較
| 手法 時間間隔 |
計算時間(sec) |
| 3次元差分法 Δt = 1μs |
818 |
| Mindlin板モデル Δt = 5μs |
79 |
| Mindlin板モデル Δt = 1μs |
233 |
このようにMindlin板モデルで計算するほうが効率が良いことがわかります。また2次元Mindlin板モデルでの計算においてタイムステップを大きくとった場合もほとんど結果がかわりませんでした。高架道路や高架軌道などのように大規模構造物の振動を計算する場合には、Mindlin板モデルを用いた手法が適しているようです。
計算結果全体の様子を見るために、計算で得られた平板の中立面の速度成分を積分して垂直方向変位を求めました。面全体の変位の平均値を差し引いて、垂直方向変位分布を5000倍に拡大して図4に示しました。
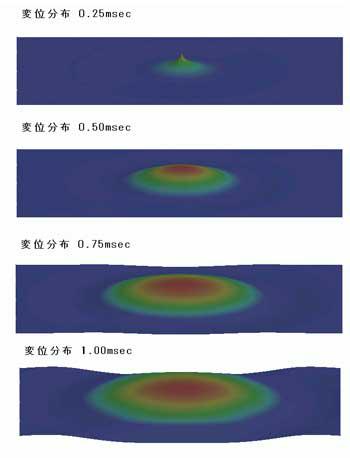
図4 変位分布、加振点中央
以上のように衝撃加振力に対する平板の振動が3次元解析によっても予測できることがわかります。3次元解析を行うことで材質の不均一性等や断面内の応力分布等の評価も可能になります。したがって解析対象の性質、注目する物理量によって手法の使い分けが必要です。
5. まとめ
以上のように2次元Mindlin平板モデルを用いても、3次元固体力学を用いても平板の振動が計算できることを示しました。どちらの手法を用いても、同等の結果が得られることが示すことができます。従って計算効率を考えると、大規模構造物の振動予測を行う場合は2次元Mindlin板モデルを用いて予測計算を行うことが適しているようです。今後、実験による数値シミュレーション結果の検証などを行う予定があります。また振動速度分布から、放射音の数値予測を試みようと考えています。
参考文献
-
宇野享: FDTD法による電磁界およびアンテナ解析 (2002) コロナ社.
-
S. K. Lele: Journal of Comp. Physics 103 (1992) 16.
-
R. Iwatsu et. al: Proeedings of 13th International Congress on Sound and Vibration, Vienna (2006) SS38-3
-
岩津玲磨、鶴秀生: 数理解析研究所講究録. 1529 (2007) 1
-
Karl F. Graff, Wave Motion in Elastic Solid (1991) Dover Publications.
-
近藤恭平, 振動論 (1993) 培風館.
-
鶴秀生、中島弘史, 日本シミュレーション学会19回計算電気電子工学シンポジウム (1998) pp. 21-24




