技術部 鶴 秀生
1. はじめに
現在コンピューターを使用せずに、音響解析を行うことは特殊な場合を除いてほとんど不可能といっても過言でないでしょう。 コンピューターの使用法を大きく分けると、測定データを解析することとシミュレーション等の数値計算をすることに分類されます。 どちらの場合でもコンピューターで視覚的にデータを表示することは解析を進めるにあたって有効な手段となります。
また、視覚的にデータを表現する為のコンピューターグラフィックスのさまざまな手法は音響の数値シミュレーションを行う場合にも適用できる場合があります。 例えばコンピューターグラフィックスでのレイトレーシングや影の計算などのテクニックは、 建築音響や電気音響のシミュレーション等の計算に直接応用ができます。これは光も音もともに波動方程式に従うことに関係しています。
さらに、音の測定データを解析する場合にも、特に時間的に変動する音を解析する場合には、 周波数の時間変化等を表示する2次元以上のグラフィックが必要になります。
ここではコンピューターグラフィックスの簡単な説明と具体的な例を紹介します。
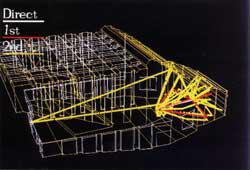
図1 虚像法による計算例
2. コンピューターグラフィックス
コンピューターの低価格化と高速化とXWindowシステム等の標準化によって、 ワークステーションによるコンピューターグラフィックスが比較的容易に行えるようになってきました。 しかしながら実際にコンピューターグラフィックスを作成し、また動画化等を行うにあたっては、以下の問題点を解決する必要があります。
- 画像情報は大容量のメモリーを必要。
例えばテレビの1画面は640*500*3で約1メガバイト。 - 陰面処理、遠近法、レイトレーシング、シェーディングなどを行って、コンピューター画面を作成するのには多くの計算量とメモリーを必要
- 影の計算や図形どうしのブール代数等には複雑なアルゴリズムが必要
- 一般のテレビの画面の信号はNTSC方式(コンポジット信号) でXWindowなどのコンピューターの画面の信号はRGB方式でしかも走査線の数や解像度も違うのでビデオ等に記録する場合には信号を変換する必要
問題点 1.~3. を解決する為の技術が実は音響解析にも応用できることがよくあります。 例えば大容量の画像情報の圧縮技術にFourier変換やWavelet変換などが応用されていて、 この情報圧縮の技術は音声の情報圧縮や特徴抽出にも応用が考えられています。 また以下の例で示すように問題点 2.~3. での計算でのアルゴリズムは音響シミュレーションに直接適用できる場合が数多くあります。
問題点 4. に関しては信号の変換やコンピューター画面の計算に時間を要することを考慮して、 当社ではフレームメモリーを利用した駒撮りシステムを利用しています。フレームメモリーを用いるメリットは、 コンピューターのディスプレイの解像度等と関係なくグラフィック画面が作成できることです。 また途中でDA、AD変換をする回数がスキャンコンバーターを使用する場合に比べて少ないので画質が劣化しないことです。 当社では解析結果をコンピューターアニメーションでビデオどりするサービスを行うためのコンピューターグラフィックスの高速アルゴリズムやサイエンティフィックヴィジュアリゼーションの研究も行っています。
3. 建築音響のシミュレーション
ホールの残響時間や反射音の影響などの数値シミュレーションを行う為に、 虚像法や音線法などのように基本的に音波の伝搬を幾何音響的に扱う方法が一般的に使われています。 これらの計算を行う場合に室形の入力、表示、計算結果の表示等には3次元グラフィックはまさに不可欠となっています。
また、計算のアルゴリズムとして、たとえば虚像法において虚音源の計算、音線と反射面との交点の計算、 及び高速に計算するための反射面の前処理等はまさに3次元グラフィックで行われる手法そのものが適用ができます。 実際に3次元グラフィックのテクニックを応用することによって、虚像法や音線法における反射音の計算の高速化に成功しています。
これは、まず最初に多角形の各座標の最大値最小値のテーブルを作成し、 反射音の経路の直線と多角形を含む平面との交点が多角形に含まれるかどうかの判断を高速化するとともに (これはコンピューターグラフィックスでのレイトレーシングという計算を行うときによく使われる手法です。)、 高次の反射音を計算する際に多角形どうしの関係のテーブルから高次の反射に寄与しない多角形の組み合わせは、 最初から除外して反射経路を計算する方法を採用することで実現しました。
虚像法による計算例を図1に示しています。これは100面以上のホールで3次反射音の計算結果を示しています。
なお、図1(以下の図も同じですが。)については、グラフィックディスプレー上の画面を直接カラービデオプリンターに出力したものです。
4. Wigner分布とWavelet変換
時間的に変動する音波のデーターを解析するためにかつてスペクトログラムや時間窓を用いたフーリエ変換などが標準的に使われていました。 時間と周波数の2次元でデーターを表示するために、2次元グラフィック表示が一般的でした。
最近の数学の発達により新しい解析法としてWigner分布やWavelet変換などが時間的に変動する音声の分析に使われるようになってきました。
Wigner分布は相関関数のフーリエ変換のようなもので時間窓を使わなくても時間と周波数両方の情報を抽出できるものです。 ただし、実際の計算を行う場合は無限区間の積分は計算機では通常行えないので、何らかの時間窓のようなフィルターを必要とします。 またクロス項などの影響で差周波数成分にピークがでたり、分布関数の値が負になることがあり、解釈が困難な場合があります。
Wavelet変換は積分変換を行うときの基底関数をフーリエ変換と比べてより広い範囲から選択したものです。 特に時間的に変動する波等を解析するときには、局在した関数や台についてコンパクト(有限区間でのみ値が0でない)関数が選ばれ、 窓関数を用いなくても計算が行える利点が有ります。これは局在した関数で展開することが特徴抽出と関係づけられるので、 画像情報の圧縮や音声認識等での応用研究が盛んになされています。
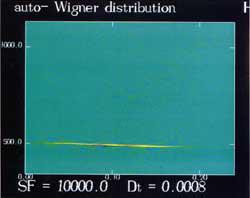
図2 移動音源のWigner分布
実際に計算を行う場合には高速フーリエ変換と同じようにアルゴリズムを工夫しないと計算時間がかなりかかりますが、 直交Waveletなどの場合にはWavelet基底のスケール関数等を使うことによって高速化が実現されています。
移動音源のWigner分布のグラフィック表示した例を図2に示します。横軸が時間方向で縦軸が周波数方向です。 この図では音源の移動によるドップラー効果も表されており、振幅が最大の位置の時刻で移動音源が受音点の直前を通過し、 その前後で周波数がシフトしていることがわかります。
5. 音響計測とコンピューターグラフィック
騒音測定などの音響計測を行った結果をグラフィックによって表示することにより、 測定の内容を測定状況とともに記録に残すことができます。
図3に航空機騒音について、飛行コースの測定結果と騒音のシミュレーション結果を、地形データとともに示しています。 空間にある曲線は観測された飛行経路を表しており、曲線の色の変わり目が表示された時刻での航空機の位置です。 地上の地形のデータの上にシミュレーション計算での騒音レベルを上書きしています。 アルファーブレンド(色の透明度を用いた重ね合わせ、色付きガラスで風景を見るようなもの) という手法を使用しているので地形とレベルを同時に表示する事ができています。 この手法はコンピューターグラフィクスにおいて3原色フルカラーが使用できて初めて実用的に実現できます。 当社ではフルカラーのフレームメモリーを利用することによって比較的簡単に実現しています。 またこの図のシミュレーションではドップラー効果等も考慮して騒音の計算を行っています。

図3 航空機の飛行コース及び騒音分布
6. おわりに
以上のように音響解析とコンピューターグラフィックスは、密接に関連し、 互いに影響を与えながら発展していくことが予想されるため、当社でも重点的に取り組んで行く項目の一つとなっています。
またコンピューターグラフィックスのテクニックは他の分野に応用できることから、 グラフィックスソフトに関しても汎用のパッケージソフトに依存せず、できる限り自社開発を行っており、 音響解析だけでなく、各種の波動解析の応用に着手しています。
詳しい説明や数式は省いたのですが、興味のある方や詳細については是非当社技術部に問い合わせ下さい。




