技術ニュース
冊子版アーカイブ

技術部 忠平 好生

1. はじめに

当社では、放送・音楽関連の各種スタジオ、コンサートホール、多目的ホールなどの良い音を追及する空間から、 残響室や無響室及び防音室などの音響計測のための特殊な空間、さらにはリスニングルームや自動車のキャビンなどの日常生活に密接した空間まで、 ありとあらゆる音空間の建築設計を手掛けてきました。

そのため当社では、以前から計算機による音場の数値シミュレーション技術に注目し、解析アルゴリズムの検討、 ソフトウェアの制作を行ってきました。その成果の代表的なものが、幾何音響理論をベースとした室内音響設計支援ソフト「コンサート」や、 工場、高速道路などの周辺の騒音伝搬を予測するソフト「ファクトリー」です。

これらの解析手法である鏡像法や音線法は、音を直進する音線として扱い、 境界で幾何反射を繰り返すことによって音が伝搬するという考えに基づいています。そのため計算アルゴリズムが比較的単純で、 プログラム化が容易であるというメリットがありますが、音の重要な性質である波動性を考慮していないために、 回折や干渉などの現象を捕えられないという大きな欠点もあります。そのため、 これらの手法が有効な範囲が空間の寸法に対して十分に波長の短い周波数帯域に限定され、 主な用途が初期反射音の伝搬経路や反射板のカバーエリアの検討などに限られているのが実状でした。 これらの手法で計算できない固有振動の影響が顕著な低周波数域の音響性状の予測は、当社の音響設計担当者を悩ませる大きな問題であり、 これを解決する音場シミュレーションシステムの構築が緊急に求められていました。

そこで当社では、近年のコンピュータ技術の発達に伴って注目度が高まっている波動音響理論に基づいた音場解析手法の基礎研究に着手しました。 当社で採用した手法は、境界積分方程式法と呼ばれるもので、境界要素法の支配方程式に波動方程式を適用して波動音場を解析するものです。この研究の結果、

1. ディジタル信号処理の導入による独自の過渡音場計算手法の構築
2. 境界条件の適用方法の改良による基礎方程式の適用範囲の拡大

などの成果が得られたと考えています。

今回は、1.についての概略と従来の幾何シミュレーション手法との対比に焦点を絞ってご紹介させていただきます。

2. 境界積分方程式法とは

境界積分方程式法の研究は、我が国では京都大学の寺井先生や大阪工業大学の河井先生らが古くから従事されており、 定常音場及び過渡音場解析の定式化をまとめた論文が数多く発表されています。本手法の基礎方程式となるのがHelmholtz-Kirchhoff積分方程式であり、 空間内の唯一の点音源Sが角周波数ωの正弦波で定常に駆動する場合、受音点Pでの定常音場を次のように表すことができます。

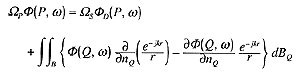(1)

ここで、Φ(P)は受音点Pの速度ポテンシャル、ΦD(P)は受音点Pでの音源Sからの直接音、n_Qは空間を取り囲む境界B上の点Qでの内向き法線、 rはPQ間の距離、k(=ω/c)は波数を表します(cは音速)。またΩ_PとΩ_SSはそれぞれPとSでの放射立体角を表し、 境界Bの内側にある場合4π、B上にある場合2π、Bの外側にある場合0となる定数です。各記号については図1を参照してください。 この式は、Greenの公式に含まれる2つの連続な関数が波動方程式を満たすと仮定して、音源や受音点などの極となる点を取り除くことにより導かれます。 この式が表すように、空間内の任意の点の音場は、音源からの直接音と境界からの寄与を加算することによって求めることができます。

また、(1)式を逆Fourier変換すると次のような過渡音場に関する積分方程式が得られます(tは時刻)。

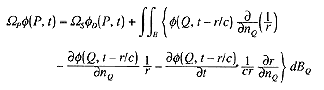(2)

ここで、φ(P)、φ(Q)、φ_D(P)は、それぞれΦ(P)、Φ(Q)、Φ_D(P)の逆Fourier変換を表します

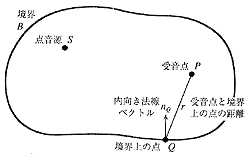
図1 境界積分方程式で使用する各記号

さて、これらの積分方程式を計算機上で数値的に解くには、積分の離散化や境界条件の適用などを検討する必要があります。 まず、(1)式を用いた定常音場の計算方法を簡単に説明します。

(1)式にはΦ(P)、Φ(Q)、及び∂Φ(Q)/∂n_Qの三つの未知変数が含まれるため、このままでは解くことができません。 そこで、まず受音点Pを境界上に置くことにより、境界上の音場に関する積分方程式を用意します。 また、境界値問題の解法を用いることにより、∂Φ(Q)/∂n_QをΦ(Q)の関数として表します。これらの操作によって、 Φ(P)∈Φ(Q)、∂Φ(Q)/∂n_Q=f[Φ(Q)]となり、式中の未知変数をΦ(Q)の一つのみに変換することができます。

このような積分方程式は第二種Fredholm型積分方程式と呼ばれ、一般的な離散化手法によって解くことが可能です。 そこで、対象とする周波数に応じた大きさの面積要素に境界を分割して積分の離散化を行い、各要素上では速度ポテンシャルが一定であるものと仮定します。 これにより要素の総数をN個とすると、式中に含まれる未知変数の数もN個となり、また一要素につき一つの方程式が得られますので、 N元の連立一次方程式を構成することができます。これを解けば境界上の音場が求められますので、 得られた値を受音点Pが空間内にある場合の積分方程式に代入すれば、所望の音場解析が完了することになります。

過渡音場解析については、大きく分けて次の二つのアプローチがあります。 一つは(1)式による定常音場解析を一定の周波数間隔を決めて各周波数毎に行い、その結果を逆Fourier変換する方法です(以下ではIFFT法と呼びます)。 また、もう一つは(2)式を用いて時間応答を直接計算する方法です(以下では直接法と呼びます)。 IFFT法は、最近では東北大学の高根先生らが研究を進めており、周波数を制限して解析できることや、 周波数毎に計算精度をコントロールできるなどの長所がある一方、 結果として得られる応答全体の長さを越えるFFT長を必要とするため十分に細かな周波数間隔を設定する必要があり、 その結果計算量が多くなるという問題点があります。また、周波数応答を逆Fourier変換する際に回り込み誤差が生じる危険性もあります。

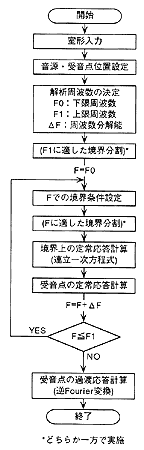
図2 IFFT法の計算フロー

一方直接法は、IFFT法とは対照的に初期応答だけを解析できるという時間軸に対する自由度があり、 少ない計算量で必要な解析を行えるという長所があります。この方法については、 先に述べた寺井先生や河井先生らが三角波応答を計算する手法を定式化しています。 これは、サンプリング周期を指定して各サンプル毎の応答を過去から未来へ逐次計算するものです。 ]そのため、サンプル間に到来する波を見逃す危険性があり、音源信号に変動の少ない関数を使用するなどのテクニックを駆使してこの問題を回避しており、 計算アルゴリズムがかなり複雑になっています。また発表されているいくつかの報告の中で、 時刻が進むと応答の乱れが生じて解が収束しないという問題が指摘されており、応答を時間軸上で平滑化したり、 法線方向微分型の積分方程式を用いることにより解の安定性を向上させることができるとしています。 しかし、変動の少ない信号の使用や時間軸上での平滑化は、高い周波数ほど計算精度が低下するという欠点を生じると考えられます。

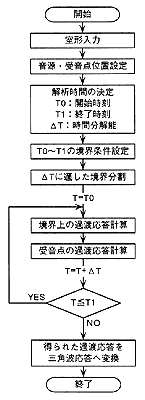
図3 直接法の計算フロー

(2)式を用いた過渡音場解析の手順は、先に述べた定常音場の解法とほぼ同様です。 (2)式には、φ(P)、φ(Q)、∂φ(Q)/∂n_Q、∂φ(Q)/∂tの四つの未知変数が含まれますが、 先の三つについては(1)式に行った操作と同様にしてφ(Q)に変換が可能で、 また最後の∂φ(Q)/∂tについても微分の定義式から近似的にφ(Q)の関数で表すことができます。 後は同様に境界の離散化を行い、さらに時間軸の離散化を行うことにより、数値解析可能な境界上の音場を求めるための方程式を導出します。 ところで、(2)式の右辺に含まれるすべての未知変数は、左辺のφ(P)に対してr/cだけ過去のものです。 このことは、ある時刻からシーケンシャルに数値計算を行う際には、右辺が既知であることを示しています。 したがって、(1)式で使用した連立一次方程式を解くステップが不必要となり、記憶容量の少ない計算機でも計算できることになります。

3. 過渡音場の解析手法について

前項で、境界積分方程式法による過渡音場解析の二つのアプローチの概略を説明しましたが、 双方に長所と短所があり、目的に応じてこれらの方法を使い分ける必要があると思われます。建築音響設計のツールとして考えた場合、 主な設計指標であるC値やD値などの定義に見られるように初期の応答が重要になります。 また早急な実用化を考えた場合、汎用の小型コンピュータで計算できると好都合です。 これらの条件を考慮すると、直接法の採用が現実的であると考えられます。

IFFT法については既に実用化されている定常音場の解析手法を利用することができますが、 直接法は前項で紹介した河井先生らの手法が発表されている程度であり、未だに研究段階であると言えます。 また、この手法にはいくつかの問題が残されています。そこで、著者は新しい直接法のアルゴリズム開発を試み、 従来の手法よりも簡単で、しかも任意の離散信号を音源に入力できるなどの自由度の高い手法を構築することができました。

以下では、解析手法の発案に至った経緯とその解析手順のアウトラインを簡単に説明させていただきます。

解析アルゴリズムを検討する際に最も注意したのは、(2)式の右辺に含まれる各関数のr/cの遅延計算をいかに精度良く行うかという点です。 実際の計算機を用いた数値計算では、サンプリング定理に基づいた離散信号を扱うことになります。 したがって、遅延時間r/cがサンプリング周期の整数倍になる場合には単に数列のシフトで良いことになりますが、 それ以外の場合にはサンプル間に到来する波を見逃さないためにサンプル間の信号を精度良く補間する必要があります。 そこで、この問題に対処するために、ディジタル信号処理の概念を積極的に取り入れることにしました。 ディジタル信号処理の理論では、信号が折り返し成分を持たない、即ちナイキスト周波数(サンプリング周波数の二分の一)以上の成分を持たないならば、 連続信号と離散信号は完全に一対一に対応します。したがって、既知の離散信号から連続信号を求めることが可能で、 任意の時刻の正確な応答を得ることができる、即ち任意時間の遅延を正確に計算することができます。 但し、この関係を利用するには、離散信号の全体が既知であり、有限の長さを持っているという条件が必要になります。

そこで、数値計算手順の第一段階である境界上の音場を計算する過程において、(2)式を次のように分割して計算することを考えました。

I 直接音の計算

音源に有限の長さの離散信号を入力し、この信号が音源から放射されて境界上の各点に到達するまでの過程を次の(3)式により計算します。

(3)

ここで、φ[0](P)は境界上の点Pでの直接音による応答を表します。

II 反射音の計算

ステップIの計算完了後は、音源はすべての信号を放射してしまったので、無視して良いことになります。 一方、境界上に音源から放射された信号が分布していますので、 次のステップではこれらの境界上の信号が音場内に再放射されて他の境界上の点へ到達するまでの過程を次の(4)式により計算します。

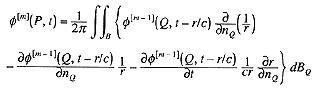(4)

ここで、mは反射次数と対応し、ステップIの直後ではm=1となります。したがって、φ[m](P)は境界上の点Pでのm次反射音による応答を表します。 これ以降は、mを更新して(4)式による計算を繰り返し行うことにより、各反射次数の境界上の点での応答が求められます。

III 直接音と各反射音の合成

必要な反射次数までステップIIを繰り返し、最後に(5)式で直接音と各次の反射音を加算すれば、境界上の点での応答が得られます。

(5)

以上の手順で境界上の応答が計算できますので、その後音場内の所望の位置に受音点を置いて、 音源からの直接音と境界からの寄与を加算すれば音場解析が完了します。

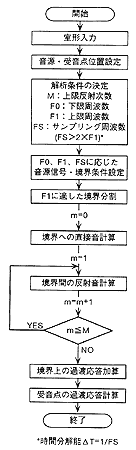
図4 本手法の計算フロー

この解析手法の特長をまとめると次のようになります。

1. 音源信号にはサンプリング定理に関するもの以外の制約を受けることがなく、任意の有限長の離散信号を入力可能(自由な周波数選択性)。
2. 鏡像法や音線法などのように反射次数を単位とした解析結果を導出するため、これらの幾何的な手法との比較が容易。 また、適当な次数で計算を打切り、初期応答だけを計算することが可能(自由な時間選択性)。
3. 指定したサンプリング周期による上限周波数以下の範囲では精度の劣化がなく、 サンプル間に到来する波についても忠実な推定が可能(各周波数を通して均一な計算精度)。
4. 各計算ステップをFFTを利用して周波数領域で行うことが可能(畳み込み演算、遅延計算の高速化)。

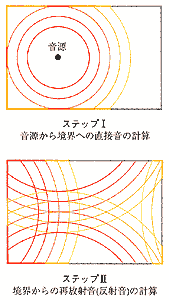
図5 計算手順のイメージ

最後の特長は特筆すべき点であり、ディジタル信号処理の考え方を取り入れたことによる恩恵とも言えるべき長所です。

また、定常音場解析のように連立一次方程式を解く必要がなく、パーソナルコンピュータ程度の能力でも、 メモリの少ない計算機でも、十分に実用に耐えるプログラムを作成できます。

さらに、この解析アルゴリズムは並列処理にも適しており、使用する計算機やプログラミング次第で計算の高速化を計ることも可能です。

ここで述べた独自の過渡音場解析理論の詳細は、音響学会誌に掲載された論文(51巻3号、191～201項、1995年)の中にまとめてありますので、 興味のある方はそちらを参照してください。

4. 検証実験結果の紹介

I 剛な矩形板の反射特性

新しい過渡音場解析アルゴリズムの検証のために、まず簡単なモデルとして、 自由空間に浮かぶ剛な矩形板に無指向性点音源から球面波が入射するときの音波の反射性状を対象とした数値計算を行い、実測値との比較を試みました。 実験ではこのような音場を無響室内に2枚の矩形板を配置し、音源に12面体スピーカを用いて模擬しました。 実験のブロックダイアグラムは図6に示すとおりです。

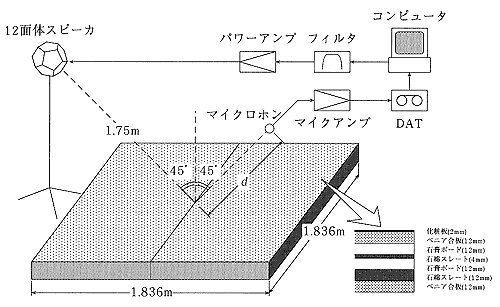
図6 実験Iのブロック図

2枚の矩形板の中心点を音波の入射点と見立てて、マイクロホンの位置を鏡面反射方向に距離を0.6m、1.5m、2.5mと変えて、 M系列-高速アダマール変換法によりインパルス応答を測定しました。なお、サンプリング周波数は48000Hz、M系列信号の長さは65535ポイント、 同期加算の回数は15回としています。ただし、使用した12面体スピーカの特性が1000Hz以上で指向性を持ち、 また80Hz付近で無響室の固有モードが顕著であったため、音源への入力信号を100～1000Hzのバンドパスフィルタにより帯域制限しました。 また数値計算では、音源入力信号として実験に用いたスピーカの特性を測定したものを使用しました。

計算でのサンプリング周波数は4000Hzとし、矩形板の表面を40×40個の正方形要素に分割して行いました。

図7に示す結果から、各点の実測と計算の時間応答が良く一致していることがわかります。 また、得られた時間応答をFourier変換して周波数特性を求めて見ましたが、その結果からも大きな差は確認できません。

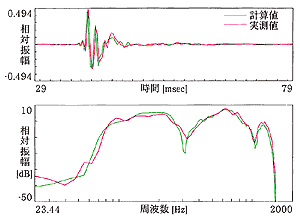
図7(a) 実験結果 ... 受音点 d=0.6m

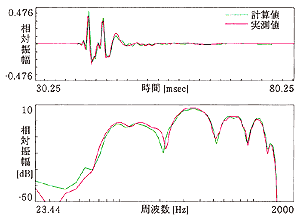
図7(b) 実験結果 ... 受音点 d=1.5m

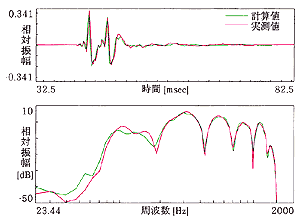
図7(c) 実験結果 ... 受音点 d=2.5m

II 残響室内の矩形パルス応答(鏡像法との比較)

実験Iでは、平らな矩形板の表面だけを解析対象としましたので、数値計算では一次反射波のみを計算しています。 そのため、反射次数の増加に伴う演算誤差の蓄積の度合いや、解の安定性を確認するには至っていません。 そこで次のステップとして、剛壁で囲まれた残響室を対象として数値計算を行い、実測値との比較を行いました。 また、音楽ホールなどの音場シミュレーションツールとして実用されている鏡像法でも同様の数値計算を行い、 音の波動性を考慮した音場解析の有効性を検証しました。

使用した測定システムのブロックダイアグラムは図8のようになります。 残響室内に設置した12面体スピーカを矩形パルスにより駆動し、サンプリング周波数1000Hzで過渡応答を測定しました。

なお、音源への入力信号は、数値計算における計算量の問題とS/Nの確保のために、 100～300Hzのバンドパスフィルタで帯域制限しています。また実験Iと同様に、数値計算での音源入力信号には、 12面体スピーカの矩形パルス応答を無響室にて測定したものを使用しました。計算でのサンプリング周波数は1000Hz、 境界は3546個の四角形要素に分割し、境界上の応答を八次反射まで計算しました。

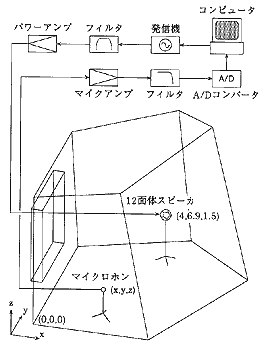
図8 実験IIのブロック図

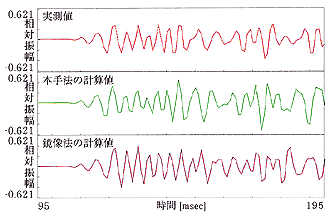
図9(a) 実験結果 ... 受音点(2,1,1.2)

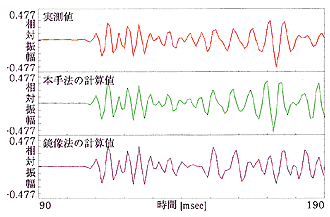
図9(b) 実験結果 ... 受音点(3,3,1.2)

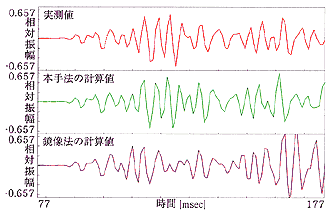
図9(c) 実験結果 ... 受音点(4,5,1.2)

鏡像法では、同様に八次反射までを計算してエコー・ダイアグラムを求め、 これに音源入力信号を畳み込んで矩形パルス応答を算出しました。受音点の位置は図8に示す三つです。

図9に示す結果を見ると、本手法の計算結果は実測値に良く一致しています。 一方、鏡像法の結果は、各受音点において直接波が到来してから20～30msecまでの区間では実測値及び本手法の計算値と良く一致していますが、 それ以降に誤差が生じているのが確認できます。これは、反射面の寸法と波長の関係による影響や、 対象とした残響室の形状が不整形であるために生じる音線経路の影による誤差が原因として考えられます。

反射次数毎に誤差の要因を具体的に考察すると、以下のようになります。

1. 一次反射音で生じる誤差

   対象とした残響室には透過損失を測定するために設けられた試料面があり、 音源の位置によってはその淵の部分に鏡面反射点が隠れてしまう場合があります。このような場合には、 エッジからの回折波だけが受音点に寄与するため、波動性を考慮しない鏡像法では計算することができません。

2. 二次反射音で生じる誤差

   一次反射音と同様な試料面による回折波に加えて、 残響室の不整形であるために隣接した二つの壁の間の二次の鏡像に対して影になる領域が存在するので、 これによる回折波についても鏡像法では計算できません。

3. 三次以降の反射音で生じる誤差

   一次、二次反射音で生じる回折波も増加していきますが、さらに以前の次数で生じた誤差も反射を重ねる毎に蓄積されていきます。

   したがって、鏡像法に限らず幾何的な考え方に基づいた解析手法では、 対象とする空間の形状が複雑になり、反射面の大きさが波長に比べて小さくなるに伴って誤差を生じる危険性が高まることになります。 実際の劇場、音楽ホール、録音スタジオなどの音場を解析対象とするには、このような条件を避けて通ることは不可能であり、 これからの音場解析では音の波動性を考慮することが主流となってくるでしょう。

図10 剛な矩形板の反射特性実験

5. おわりに

新しく開発した境界積分方程式法による過渡音場の解析手法の概要について紹介してきましたが、 本手法の実用化に際して大きな問題が残されています。それは、壁や天井などに取付ける建築材料の吸音特性のデータベースをどのように収集するかです。 過渡音場の数値解析では、吸音材の時間応答特性が必要になります。現在、一部のハンドブックなどに掲載されている吸音データは、 吸音率の1/1あるいは1/3オクターブバンドの周波数特性がほとんどです。 このようなデータには反射の際の位相遅れに関する情報は含まれていませんので、時間応答を算出することはほとんど不可能であると言えます。 したがって、吸音材の時間応答特性に関するデータベースを新規に構築する必要があり、またそのための測定方法についても検討しなければなりません。 本手法による音場シミュレーションを当社の業務に活用するためには、これらの課題を早急に片付ける必要がありますが、 なかなか良いアイデアが浮かばず、少々停滞気味になっています。どなたか同じような経験のある方や、この問題を扱った文献を調査された方は、 ご教授していただければ幸いです。

また今後は、本手法を用いた音場シミュレーションソフトウェアを作成し、 これを当社の業務に活用して以下のようなサービスを提供していきたいと考えています。

1. 室内音響設計・施工業務への応用

   これまで困難であった低周波数域での音響障害の予測が可能になり、設計段階でその対策を施せることから、 設計施工の効率化を図ると同時に、さらに良い音響空間を実現できるようになります。

2. 音場シミュレーションの受託

   音響空間の形状検討、効果的なスピーカ配置、 アクティブノイズコントロールのシミュレーションなどで早急に対象となる音場の特性を把握されたい方に、音場シミュレーションを実施します。

3. ソフトウェアの販売

   お客様のご要望に応じてプログラムをカスタマイズし、販売させていただきます。 また、市販の境界要素法ソフトウェアをお持ちの方には、そのプログラムとのリンクも検討いたします。

これ以外にも色々な御相談に応じます。本研究の成果が、あらゆる音響分野に適用できる優れたツールとして機能することを目標として、 さらなる検討を進めていく所存です。今後に御期待ください。

謝辞

本研究に関しては、東京電機大学の浜田晴夫助教授の御指導を頂きました。 また実験に関しては、(株)奥村組筑波研究所の飛松様、木村様の御協力で残響室及び測定システムを貸与して頂きました。 以上の方々をはじめ関係者各位に心から感謝いたします。