技術部 鶴 秀生・忠平 好生
1. はじめに
境界要素法は、種々の分野で解析手法として使われていますが、音響分野でも、ホール、スタジオ内、 防音壁回りの音場の計算などに応用されています。当社では、音響分野での境界要素法や音源探査等の逆問題の知見を活かし、 この度、コンカレント日本社が開発した心理生理現象解析評価システム(AEPPS) のオプションとして用意されている『BEM-逆問題モジュール』を共同開発しました。
ここでは、境界要素法と心理生理現象との関係及びそれらの音響心理実験への応用の可能性等について紹介させていただきます。
従来の音響心理実験においては、まず音を呈示し、それから受けた感想を複数の人にアンケート記入してもらい、 その結果を因子分析法等の統計処理し、評価する方法が一般的に用いられています。
これらの作業を迅速かつ効率的に行うのが、当社の音響心理実験システム「真耳(しんじ)」です。 このシステムは、パーソナルコンピュータを用い、呈示音の取り込み、加工、呈示を行うとともに、被験者側の端末を通じたデータの回収、 集計統計処理を一括して行うものです。
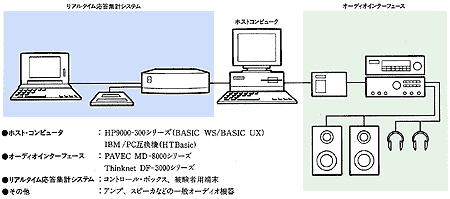
図1 真耳のシステム構成図
しかし、従来からの心理実験も真耳システムも、被験者の感じた印象を、与えられた表現語に沿って評価する、 ある意味で二次的な印象を統計処理するもので、被験者の持った直接的な印象や細かなニュアンスを把握することは困難です。
従来から脳の機能と心理現象の間に密接な関係があることが知られています。今回の試みは、その関係に注目し、 様々な環境下における脳の内部の神経活動の状況を把握することによって、より深く様々な心理現象を解明しようとするものです。
まず第一に脳の活動のデータをいかにコンピューターに取り込むかという問題がでてきます。 生きた人の頭を割って脳の中身を見ることはできませんし、例え見たにしても、どの様に活動しているのか分かりません。 そこで、間接的に得たデータより脳の状態を調べることが必要になってきます。
最近、脳の神経細胞の活動に伴った頭皮上の電場や磁場の変化を観測し、脳内のどの領域の神経細胞が活動をしているかを特定し、 製品開発に結び付ける研究が盛んに行われるようになりました。
これは、人間の頭部を多層構造を持った電気伝導体と考え、活動している神経細胞群を電流双極子とみなし、 双極子の位置とモーメントを推定するもので、この手段としては、静電場の基礎方程式を境界要素法逆問題を用いて解くことが最も有効と思われます。
以下、脳機能逆問題について、活動電位とデータの取り込み、境界要素法、逆問題についての詳細とシステム全体の構成についてご紹介します。
2. 活動電位とデータ取り込み
脳の活動は、神経細胞の興奮によって誘発される電気的な信号(EVOKED)と頭皮上の電位を連続的に追跡した脳波(EEG)で特徴付けられます。 この2つが心理生理現象解析評価システムの入力対象となります。
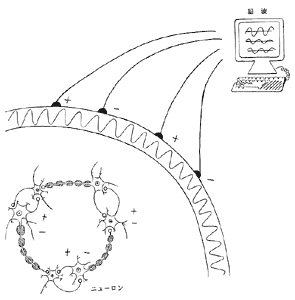
図2 脳の神経細胞の活動と脳波の図
脳波はコンピュータに登載したA/Dコンバータによりデジタル値に変換することで各種解析を行うことが可能になります。 本システムの入力スペックは次のとおりです。
- 多チャンネル:標準64CH、最大128CH同時取り込み可能
- 高速性:5kHz/CH以上
- 高分解能:標準で12bitA/D、オプションで16bitA/Dをサポート
本システムの解析機能としては、得られた多チャンネルのデジタル信号をもとにスペクトル解析や、 ゆらぎ解析、脳波の2次元マッピング表示などもリアルタイムに行われるようになっています。
次に、実際に脳のどの領域が活動しているかを推定するためのアルゴリズムである境界要素法及び解析手法について説明します。 なお、数式を見ると眠くなるという方は以下の2節は飛ばして、システムの構成の部分からお読み下さい。
3. 境界積分方程式
まず、静電場の電位φの基礎方程式としてPoisson方程式
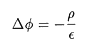 (1)
(1)
を考えます。ここでρは電荷密度、εは誘電率です。
この方程式の基本解u*は
![]() (2)
(2)
を満たします。3次元の場合は
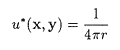 (3)
(3)
でrはxとyの距離です。この基本解の領域の境界での法線方向の微分を
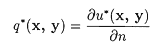 (4)
(4)
で表します。境界条件を電位uと電位の法線方向微分qで与えるとき次のような積分方程式でPoisson方程式は表現できます。
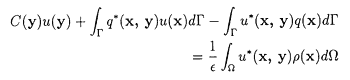 (5)
(5)
ここでΩは領域をΓは領域の境界を表し、また
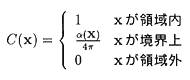 (6)
(6)
でαは境界上の点から見た領域の立体角です。この積分方程式を離散化し、 境界条件と電荷分布を与えることによって領域内の電位uに対する数値計算を行う事ができます。
また離散化したときの各境界要素についての境界条件を電位のみまたは電場の法線方向成分のみを与えたときでも 方程式(5)の点yを各境界上の要素に一致させる事によって得られる連立方程式を解く事によって境界条件を得る事ができます。
次に多媒質系での境界要素法については、誘電率εjの領域ΩjがΓjとΓj+1で囲まれていて、 各ΓjがΓj+1を囲むような多層構造の媒質を考えます。
これは頭部を脳、頭蓋骨、頭皮などの領域による多層構造でモデル化していることに対応します。
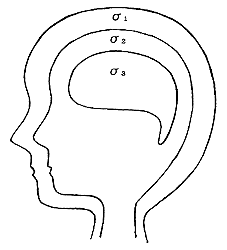
図3 頭の多層構造モデル
各境界Γj上の点yに対して
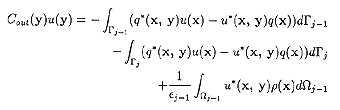 (7)
(7)
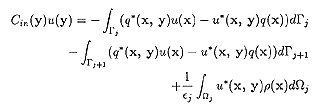 (8)
(8)
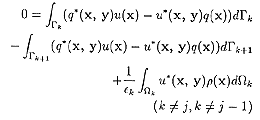 (9)
(9)
が得られます。境界はΓ1~Γnで,境界Γ1の外側の領域の誘電率がε0のとき、上の各式にそれぞれεj、εj-1、εkをかけてたしあわせることによって
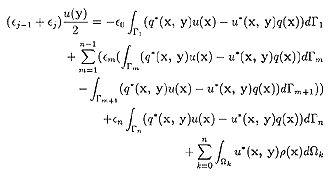 (10)
(10)
が得られます。境界層に表面電荷がない場合は上の方程式は
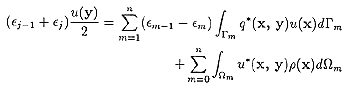 (11)
(11)
となります。この方程式を離散化する事によって得られる連立1次方程式を解く事で各境界面要素の電位が計算できます。 ここでは離散化に際して境界面要素内での電位u(x)を要素の頂点の値で線形に近似する一次要素法を用いることにし、 各要素の頂点を節点として離散化を行います。
各要素頂点での電位ベクトルをUで表し方程式を行列表現すると
HU = F (12)
となります。
ここで行列Hは
 (13)
(13)
各Hijは行列で
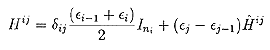 (14)
(14)
Iniはni×niの単位行列で、各Hijは行列で各mn成分は
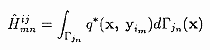 (15)
(15)
で計算されます。Yimは境界面上の要素の頂点で第m番目のものの座標となります。またFはベクトルで
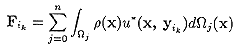 (16)
(16)
となります。もし電荷分布が位置xjにあるモーメントdjの点双極子j=1, ndの和で表現できる時Fは
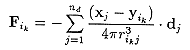 (17)
(17)
となります。ここで
![]() (18)
(18)
です。
4. 逆問題
前節の系で要素上の電位を測定し、ソースである電荷分布を推定する問題を考える事にします。
たとえ境界上の要素全ての電位が与えられたとしても、電荷分布は一意的には定まりません。 本解法では電荷分布を数個の点双極子で近似できるものと仮定し、各双極子の双極子能率と位置を推定することにします。 電位の測定点をn個、要素の頂点に一致させるような位置にとり、各測定点の対応する頂点番号をji, (i=1, n)で表わし、 その測定値をv(i), (i=1, n)とします。
そのときm個の双極子の位置と双極子能率をrk,dk(k=1, m)と仮定したとき各測定点iで得られる電位を
w(i) = w(r1, ......., dm) (19)
で表わします。前節での行列Hの逆行列Gとm個の双極子から得られるベクトルFによりw(i)は
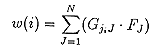 (20)
(20)
で計算されます。Nは頂点の総数で、このw(i), v(i)によって得られる残差res
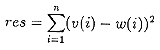 (21)
(21)
を最小にするように双極子の位置とその双極子能率を推定すればよいわけです。実際FJは
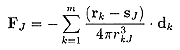 (22)
(22)
となります。なおsJは各頂点の位置ベクトルを表します。よって、双極子の位置が定まれば計算値をw(i)をベクトルwで表示すれば、行列を使い
w = MD (23)
で表現できることがわかります。Dは3m次元のベクトルで
D3j+1 = djx, D3j+2 = djy, D3j+3 = djz (24)
Mはn行3m列の行列で成分は
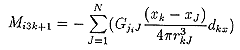 (25)
(25)
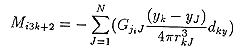 (26)
(26)
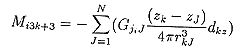 (27)
(27)
で表現されます。ここでxk, yk, zkはk番目の双極子のx, y, z座標でxJ, yJ, zJはJ番目の頂点のx, y, z座標です。 双極子の位置が仮定されれば残差resを最小にする双極子能率ベクトルDは行列Mの一般化逆行列Wを使って
D = Wv (28)
となるので、残差は双極子の位置rkだけの関数となります。したがって、 残差を小さくする方向に双極子の位置を移動させながら双極子の双極子能率と位置を推定することができます。
乱数で選んだ初期値からより適切な数値解を求める解法として、ニュートン法の拡張版とも言えるLSB法を用いることができます。 しかし、ある初期値から収束した双極子の位置と双極子能率が必ずしも最適な値を与えるとは限りません。 それは残差が多数の点で局所的な極小値を持つことがあるからです。LSB法では、 残差が局所的な極小値になるとそれ以上値が改善するようにパラメータを変化させることができません。
そこで、LSB法で収束した後、その収束した点から別の点に乱数で移動させて、 移動された点からLSB法を使い収束させた点での残差と前の収束点での残差を比較し、 もし新しい点での残差が小さいときには新しい収束点を採用し、そうでなければ前の点を収束点として残す方法などを使います。 このことを繰り返し適当に残差が小さくなったとき計算を打ち切ることで最適値を見つけることを試みました。
これまでの説明では誘電率を用いましたが、脳波の場合は実は導電体と考えて、電流双極子をソースと考えて問題を解けば良いことが分かります。 また、これらの解析には自由度の数より多いチャンネルのデータ取り込みが不可欠であることを強調したいと思います。
最後に音響解析に境界要素逆問題を応用するには基礎方程式としてPoisson方程式の変わりにHelmhlotz方程式
Δφ + k2φ = 0 (29)
等を考えれば良いことが分かります。音響問題の場合は、電位の変わりに音圧を用いれば良いわけです。 ただし、位相をどう扱うかが難しい問題として残りますが、例えば音響ホログラフィー等の方法等で困難の解決をはかることができます。
5.5 システムの構成
「心理生理現象解析評価支援システム」(Analysis and Evaluation of Psycho-Physiologycal Phenomena Support System: AEPPS)は、 脳波をはじめ各種生体信号や騒音・振動レベルなど環境情報をリアルタイムに計測し、多面的に解析評価することにより、 複雑な心理生理現象の把握を支援するものです。
図4に逆問題解析の結果を示し、図5にシステム構成図を示します。

図4.A 表面電位分布
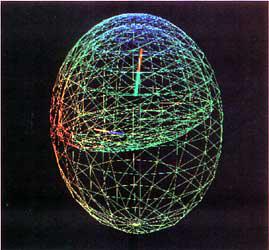
図4.B 表面電位分布による推定双極子
図4.Aには、2層モデルによる双極子による電位分布を示し、最外郭の境界はワイヤーフレームで内部の境界面は面で表示しました。
図4.Bには、2層モデルによる双極子の位置と強度の推定結果を示し、各々の境界面はワイヤーフレームで表現しています。
このシステムの具体的な応用例としては、音声認識等における脳の活動状態のモニターやコンサートホールの響きの心地よさの評価等が考えられます。 また、テレビCMや番組等が与える印象のモニターリングなどにも応用ができるでしょう。 騒音等の不快感に対するの客観的なデーターの収拾にも威力を発揮すると考えられます。
また、音響以外では車の乗り心地の評価、香の与える心理生理的な影響の研究などの支援にも一役買うことが期待できるでしょう。
6. まとめ
以上境界要素法の逆問題を用いた双極子推定手法を説明させていただきました。 ここで紹介したモジュールを用いることで心理現象をより客観的に評価することが可能になっていくものと信じています。 この様に人間の心という神秘のベールの中身を解明するシステム開発に携わることができたことを幸せに感じています。
今後、「真耳システム」と「AEPPS」をドッキングしてより包括的な音響心理実験システムを開発していく予定です。
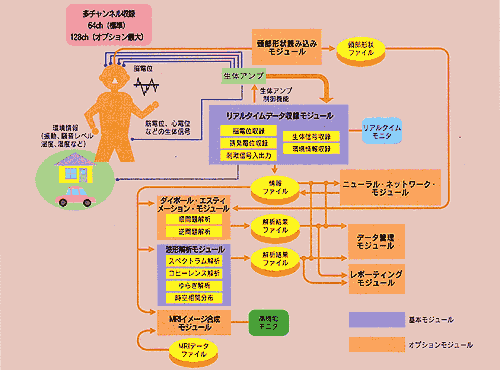
図5 AEPPSシステム図
また、境界要素法、逆問題を含め、様々な数値解析手法の開発を積極的に行うことを考えておりますので、 お気軽にご相談くださるようお願いいたします。
なお、今回ご紹介した「AEPPS」についてはコンカレント日本株式会社にお問い合わせくださるようお願いいたします。
連絡先:
コンカレント日本株式会社(営業管理部)
電話:03-3864-5713
【参考文献】
- 1. A.C. Banard, I. M. Duck and M. S. Lynn: Biophys. J. 7 (1967) 443 .
- 2. A.C. Banard, I. M. Duck, M. S. Lynn and W. P. Timlake: Biophys. J. 7 (1967) 463 .
- 3. W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery:Numerical Recipes in Fortran, 2nd Ed.(1992) Cambridge University Press.
- 4. 半谷 裕彦, 川口 健一: 形態解析 (1991) 培風館.




